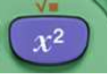Mathématiques
Racine carrée en 4ème
En appliquant le théorème de Pythagore, il est très fréquent de chercher un nombre dont on connaît le carré. Par exemple, un calcul nous permet d’obtenir que AB² = 49, et nous voudrions savoir ce que mesure AB sans le ². Nous pouvons utiliser la racine carrée. Mais ne mettons pas la charrue avant les bœufs, et revoyons d’abord la définition du carré d’un nombre.
Carré d’un nombre
Définition
Le carré d’un nombre est le produit du nombre par lui-même. Par exemple :
- le carré de 5 est égal à 5 × 5 = 25
- le carré de 7 est 7 × 7 = 49
- le carré de 10 est 10 × 10 = 100
- le carré de 1 est 1 × 1 = 1
Pourquoi appelle-t-on cela « carré » ? Quel rapport avec les carrés ?
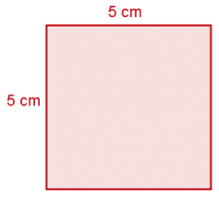
Parce que tout simplement, si vous tracez un carré de 5 cm de côté…
…son aire sera de 25 cm² (cm² se lit « centimètre carré »).
On obtient 25 en multipliant la longueur par la largeur, c’est-à-dire en multipliant 5 par lui-même.
Ainsi le produit d’un nombre par lui-même correspond à l’opération qu’il faut faire pour trouver l’aire d’un carré.
Une autre fiche est consacrée aux calculs d’aire en 4ème.
Notation ²
Si x est un nombre, son carré se note x². Par exemple, 7² = 49. 7² se lit « 7 au carré ».
Vous trouverez plus de détails sur la notation ² dans la fiche sur les puissances de 10.
Cette notation ² peut induire en erreur. Il arrive qu’on confonde le carré avec le double. Pourtant, le double de 5 est 5 × 2 = 10, alors que le carré de 5 est 5 × 5 = 25…
Les calculatrices scientifiques comportent toutes une touche « carré », souvent notée x² ou ².
Il est plus rapide de taper 46,13² plutôt que 46,13 × 46,13…
Avec les nombres négatifs
On peut calculer le carré d’un nombre négatif. Par exemple,
- le carré de - 4 est égal à - 4 × (- 4) = + 16.
- le carré de - 9 est égal à - 9 × (- 9) = + 81.
D’après les règles du produit sur les relatifs, un carré est toujours positif, même le carré d’un nombre négatif !
Cela revient en effet à multiplier un nombre négatif par un autre négatif, et le produit de deux nombres de même signe est toujours positif. « Moins fois moins égal plus ».
Le carré de - 4 se note (- 4)². Avec des parenthèses.
Si on le notait - 4², le carré étant une multiplication, il serait prioritaire, et nous devrions calculer - 4 × 4 avec un signe « moins » devant… ce qui donnerait - 16.
- 4² n’est pas le carré de - 4, c’est juste l’opposé du carré de 4.
Si on veut calculer le carré d’un nombre négatif, il faut le mettre entre parenthèses.
Les carrés parfaits
Tout comme il faut connaître les tables de multiplications pour être plus efficace, il est bon de connaître les premiers « carrés parfaits », c’est-à-dire les carrés de nombres entiers.
0² = 0
1² = 1
2² = 4
3² = 9
4² = 16
5² = 25
6² = 36
7² = 49
8² = 64
9² = 81
10² = 100
11² = 121
12² = 144
13² = 169
14² = 196
15² = 225