L’étude des fonctions dérivées permet de définir une nouvelle fonction très importante en mathématiques : la fonction exponentielle.

A la découverte de la fonction exponentielle 

La fonction exponentielle, est l’unique fonction f :

• qui est sa propre dérivée : pour tout x réel, f’(x) = f(x).
• qui vaut 0 en 1 : f(0) = 1.

Plutôt qu’avec une lettre comme f ou g, on notera cette fonction exp.
On a donc exp’ = exp et exp(0) = 1.

On peut montrer que cette fonction existe bien et qu’elle est unique.

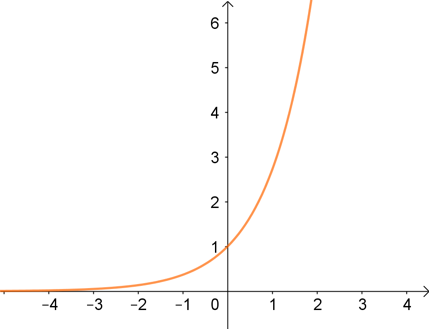
Voici sa courbe représentative :

La fonction exponentielle

exp est toujours positive, et comme elle est sa propre dérivée, elle est donc toujours croissante.

En fait, elle croît « de plus en plus vite » : plus elle croît, plus elle prend des valeurs élevées, plus elle croît davantage.

C’est même de toutes les fonctions connues jusqu’alors, celle dont la croissance est la plus rapide : même les fonctions puissances (x², x⁴, voir x¹⁰⁰⁰ !) finiront par croître moins vite que exp.

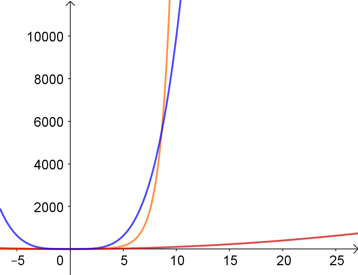
Comparaisons de fonctions

x² (en rouge) est rapidement dépassée, et même x⁴ (en bleu), qui croît pourtant très vite (10⁴ = 10 000) finit par croître moins vite que exp.

En ce qui concerne les nombres négatifs, la valeur de exp se rapproche de plus en plus de 0 sans jamais l’atteindre.

Des règles de calcul