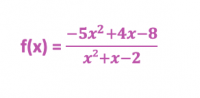Après avoir appris à calculer des dérivées, on peut (enfin !) étudier les variations d’une fonction, c’est-à-dire :

• indiquer pour quelles valeurs de x la fonction est croissante ou décroissante,
• s’intéresser aux minimums et maximums des valeurs de la fonction, à ses tangentes, voire comparer la position de deux courbes.

Tableau de variation d’une fonction

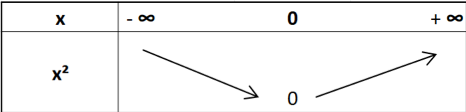
Un tableau de variation permet d’indiquer le sens de variation d’une fonction suivant les valeurs de x.

Voici par exemple celui de la fonction carrée f(x) = x² :

Tableau de variation

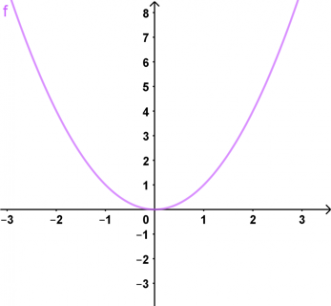
Il correspond bien à la courbe représentative :

Courbe de la fonction carrée

Voyons maintenant comment tracer le tableau de variation d’une autre fonction.

Prenons

et étudions ses variations sur l’ensemble ]-2 ; 1[.

On n’étudie les variations que sur cet ensemble car le dénominateur s’annule en -2 et en 1, et on n’a pas le droit de diviser par zéro, donc la fonction n’est pas définie en -2 et en 1.
Pour savoir où le dénominateur s’annule, on est souvent amené à résoudre une équation du second degré.

Première étape : calculons la dérivée.