Du point de vue de votre enfant, en 4^ème, le théorème de Pythagore consiste en un « outil » qu’on utilise pour calculer une longueur manquante dans un triangle rectangle.

Nous allons voir plusieurs exemples d’utilisation de cet outil.

Exemple « basique » avec Pythagore

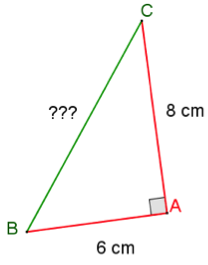
« Soit un triangle ABC rectangle en A tel que AB = 6 cm et AC = 8 cm. Calculer BC. »

On peut schématiser la question de cette façon (il est d’ailleurs recommandé de toujours faire une figure à main levée si l’énoncé n’en comporte pas) :

Nous sommes là dans le cas le plus classique du théorème de Pythagore : on travaille dans un triangle rectangle dont on connaît deux longueurs, et où il faut déterminer la troisième longueur.

Pour rédiger une réponse :

1. On commence par expliquer qu’on applique Pythagore, car le triangle est rectangle.
On sait que le triangle ABC est rectangle en A.
D’après le théorème de Pythagore :

2. On écrit ensuite l’égalité que Pythagore nous permet d’obtenir :
BC² = AB² + AC²
N’oubliez pas : dans cette égalité, le côté qui est « tout seul » est toujours l’hypoténuse ! C’est-à-dire, le côté opposé à l’angle droit, qui est le côté le plus long du triangle.

3. Une fois l’égalité écrite, on la recopie en remplaçant les noms des côtés connus par leur longueur.
BC² = 6² + 8²

4. On calcule les carrés. Attention, il ne faut pas confondre « carré » et « double » : le carré d’un nombre est égal au nombre multiplié par lui-même. Ainsi, 8² = 8 × 8 = 64.
Ensuite, on achève le calcul de BC².
BC² = 6² + 8²
BC² = 36 + 64
BC² = 100

5. Nous n’avons pas encore trouvé BC, mais nous avons trouvé le carré de BC.
Or, quel est le nombre dont le carré est 100 ? C’est tout simplement 10, car 10 × 10 = 100.
Ainsi, BC = 10 cm.

Voici la réponse rédigée sans autre commentaire :

On sait que le triangle ABC est rectangle en A.
D’après le théorème de Pythagore :
BC² = AB² + AC²
BC² = 6² + 8²
BC² = 36 + 64
BC² = 100
et ainsi, BC = 10 cm.

L’île déserte