D’un point de vue mathématique, ce théorème permet de faire le lien entre une mesure d’angle et une distance et constitue un résultat assez impressionnant en mathématiques, tout en restant accessible à des collégiens.

Le théorème de Pythagore peut s’appliquer dans de nombreux domaines (architecture, ingénierie) et a permis d’effectuer de nombreuses avancées technologiques.

Mais pourquoi Pythagore ?

Pythagore est un philosophe grec né vers 580 av. J.-C. et mort vers 495 av. J.-C. Il n’a jamais rien écrit et on ne connaît qu’assez peu de choses sur sa vie. Beaucoup d’éléments de sa pensée proviennent en fait des disciples de l’école pythagoricienne, selon laquelle toute chose était faite de nombres.

Toutefois, le théorème de Pythagore était connu dans d’autres cultures (Mésopotamie, Inde, Chine) bien avant Pythagore, et la démonstration la plus ancienne que nous connaissons provient d’Euclide, qui aurait vécu deux siècles après Pythagore. La seule démonstration rédigée par des pythagoriciens qui nous soit parvenue ne traite que d’un cas particulier du théorème.

Le théorème que nous allons étudier est néanmoins nommé en référence à cette école pythagoricienne, car ce résultat leur a permis de découvrir d’autres propriétés des nombres (par exemple, l’existence de nombres irrationnels).

Découvrons le théorème

Un théorème est une proposition qui peut être démontrée par un raisonnement logique.

En mathématiques, on utilise aussi le mot « propriété ». Les propriétés découvertes  sur les droites parallèles et perpendiculaires en 6^ème peuvent être vues comme des théorèmes.

L’énoncé du théorème de Pythagore est le suivant :

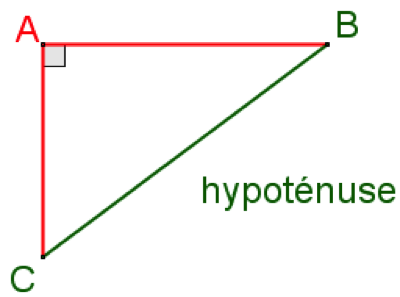
« Si un triangle ABC est rectangle en A, alors BC² = AB² + AC² »

Pour rappel, le ² se lit « carré ». Calculer le carré d’un nombre revient à le multiplier par lui-même. Par exemple, 3² = 3 × 3 = 9.
Notez que dans ce cas, le côté BC est le côté le plus long, qui est opposé à l’angle droit. On appelle ce côté hypoténuse.

On retient parfois la formulation « en français » de ce théorème, qui est :

« Dans un triangle rectangle, le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés ».

Ainsi, on établit une relation entre un angle droit dans un triangle rectangle, et les longueurs des côtés de ce même triangle. Nous discuterons de l’utilité de cette relation un peu plus loin. 

Il existe plusieurs façons de découvrir cette égalité, la plus courante étant le découpage d’aires.
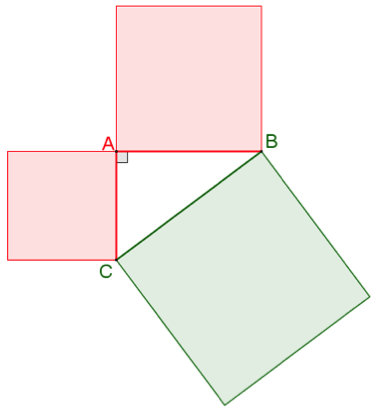
Par exemple, en traçant n’importe quel triangle rectangle ABC, et en traçant des carrés sur chaque côté :

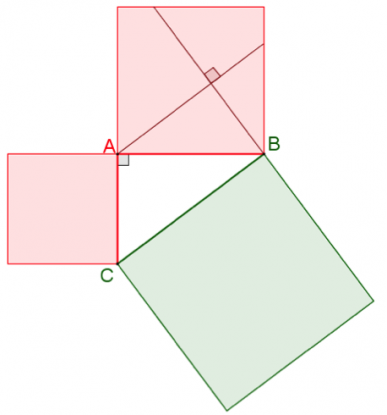
Il est possible de découper le carré construit sur le côté AB de cette façon, en prolongeant un côté du carré vert et en traçant une perpendiculaire passant par A :

et d’assembler les pièces rouges pour qu’elles se superposent parfaitement au carré vert construit sur BC.

Or, l’aire d’un carré s’obtient en multipliant le côté du carré par lui-même. Par exemple, l’aire du carré de côté AB est égale à AB².
Mais comme nous pouvons assembler les deux carrés de côté AB et AC pour obtenir le carré de côté BC, on en déduit que BC² = AB² + AC² !

Une démonstration