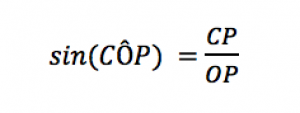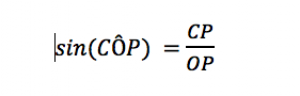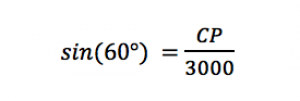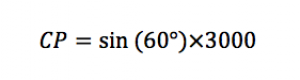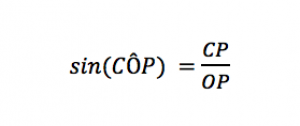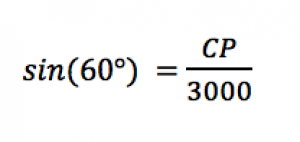Chasse au trésor

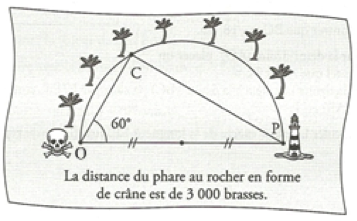
Voici une carte découverte par Ruffy, qui lui permettra de découvrir le fabuleux trésor de Math le Pirate™. 
On note : O le rocher en forme de crâne, C le cocotier sous lequel est enterré le trésor, P le phare. Le triangle OCP est rectangle en C.

Aidez Ruffy à mettre la main sur le butin en lui indiquant la distance entre le cocotier et le phare.

Pour calculer CP, on dispose des trois rapports : cosinus, sinus et tangente.

Lequel utiliser ? Cela dépend du côté dont on dispose, et du côté qu’on recherche !

On dispose de OP, qui est l’hypoténuse du triangle, et on cherche CP, qui est le côté opposé à l’angle . Et quel est le seul rapport qui relie hypoténuse et côté opposé ? C’est le sinus ! Ainsi :

L’écriture  avec les parenthèses signifie « sinus de l’angle ». 
Cette écriture avec les parenthèses (qui d’habitude indiquent des priorités de calcul) peut sembler particulière, elle correspond en fait aux fonctions également étudiées en 3ème.
Parfois on l’écrit sans les parenthèses : sin CÔP

Où en étions-nous ? A l’égalité ci-dessous :

Nous allons la réécrire en remplaçant les grandeurs connues par leur valeur.

Nous pouvons alors appliquer la règle de trois. Ainsi, 

Un petit calcul à la calculatrice (qui dispose d’une touche « sin ») nous donne CP ≈ 2598 brasses en arrondissant à l’unité.

Si vous trouvez autre chose, vérifiez que la calculatrice est bien réglée en degrés (« D » ou « DEG » apparaissent en haut de l’écran). 

Voici la solution rédigée 

On sait que le triangle OCP est rectangle en C.
Calculons :

Ainsi, 

Finalement, CP = sin(60°) x 3000 ≈ 2598  brasses.

La falaise

On reste dans le même thème avec ce second exercice plus technique :