outefois, les fonctions sont des objets mathématiques très abstraits ! C’est pourquoi elles ne sont découvertes qu’en 3^ème, puis approfondies les années suivantes.

Des machines mathématiques

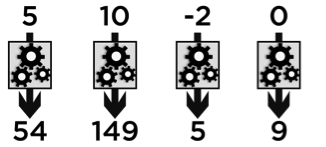
On introduit souvent les fonctions comme des programmes de calcul (ou des « machines mathématiques »), comme celui-ci-dessous :

Par exemple, si l’on choisit 5 comme nombre de départ :

• On lui ajoute 3 : 5 + 3 = 8
• On élève 8 au carré : 8² = 8 × 8 = 64
• On soustrait le double du nombre de départ : 64 – 2 × 5 = 64 – 10 = 54

Le résultat est donc 54. On a choisi 5 au départ, mais on pourrait faire fonctionner cette « machine » avec n’importe quel autre nombre.

De la « machine » à la « fonction »

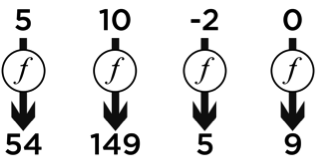
La « machine » ci-dessus s’appelle une fonction. On la représente par une lettre  (généralement f, et si on invente d’autres fonctions dans le même exercice, on les appelle souvent g, h…).

Il nous faut aussi un moyen de décrire les opérations effectuées (ajouter 3, élever au carré, etc.) sans devoir dessiner un grand cadre comme ci-dessous. 

Et ce moyen, c’est tout simplement… une expression littérale.

Si on appelle x le nombre de départ, notre fonction f :

• Ajoute 3 : x + 3
• Élève le résultat au carré : (x + 3)²
• Soustrait le double du nombre de départ : (x + 3)² - 2x

On peut vérifier que cette expression convient à notre fonction, par exemple en remplaçant x par 5 :

(x + 3)² - 2x = (5 + 3)² - 2 × 5= 8² – 10 = 64 – 10 = 54. 
On retrouve bien 54.

Ainsi, notre fonction se note f : x → (x + 3)² - 2x

On lit : « f est la fonction qui à x, associe (x + 3)² - 2x ». 
Ici, le résultat de la fonction varie en fonction de x (on peut trouver 54, 149…). x est donc appelé la variable.

On utilise aussi la notation f (x)= (x + 3)² - 2x qui se lit : « f de x est égal à (x + 3)² - 2x » qui signifie exactement la même chose.

Attention : les parenthèses de f(x) n’ont pas le même sens que d’habitude. Elles servent juste à dire quelle lettre représente la variable (le nombre de départ).

Utiliser une fonction

Prenons un autre exemple de fonction. Aux États-Unis, on mesure la température non pas en degrés Celsius (°C), mais en degrés Fahrenheit (°F). 

Si on connaît une température en degrés Celsius, il est très facile d’obtenir cette température en degrés Fahrenheit : il suffit de :

• multiplier la température en °C par 1,8
• ajouter 32 au résultat.

Appelons x une température en °C, et appelons g la fonction qui à x, associe la température en degrés Fahrenheit.

On peut donc écrire g : x → 1,8x + 32 ou bien g(x)= 1,8x + 32

Supposons que la température soit de 25°C. Qu’afficherait un thermomètre en degrés Fahrenheit ?

En utilisant la fonction g, et en remplaçant x par 25, on écrit :
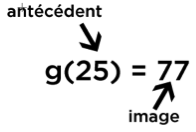
g : 25 → 1,8 × 25 + 32 = 45 + 32 = 77
ou bien g(25) = 1,8 × 25 + 32 = 45 + 32 = 77.

Ainsi, s’il fait 25°C, un thermomètre américain affichera 77°F.

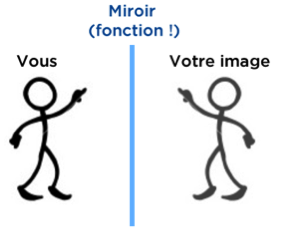
On dit que 77 est l’image de 25 par la fonction g.

En effet, lorsqu’on applique une fonction, le « nombre d’arrivée » est appelé image (de la même manière que quand vous vous regardez dans un miroir, vous voyez votre image).

Autre mot à retenir : 25 est un antécédent de 77 par la fonction g. On appelle « antécédent » le « nombre de départ ».

Voici un petit schéma pour s’en rappeler : 

Notez qu’on dit « l’image » mais « un antécédent »

Pour un antécédent donné, on ne trouvera qu’une seul image. Un même nombre de départ ne peut pas aboutir à plusieurs nombres d’arrivée différents. Mais pour une image donnée, on peut parfois trouver un, plusieurs (et parfois aucun) antécédent(s).

Ainsi, dans la fonction f vue précédemment, f(5) = 54 et f(- 9) = 54 aussi. 
54 a deux antécédents par f : 5 et – 9.

Tableaux et graphiques