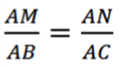Mathématiques
La réciproque du théorème de Thalès en 3ème
Le théorème de Thalès permet de calculer une longueur manquante. Il faut pour cela se placer dans un triangle muni d’une droite parallèle à un côté (ce qu’on appelle configuration de Thalès).
La réciproque du théorème de Thalès, au contraire, s’appliquera dans une figure comportant un triangle et une droite.
Elle va nous permettre de déterminer si la droite est bien parallèle à un côté du triangle. Il faut pour cela qu’on connaisse déjà certaines longueurs.
Énoncé de la réciproque
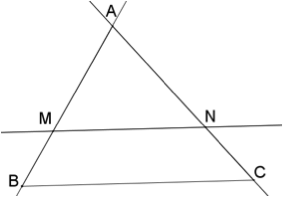
Si dans une figure,
- les points A, M et B d’une part, et les points A, N et C d’autre part sont alignés dans le même ordre,
- l’égalité suivante est vérifiée :
alors les droites (MN) et (BC) sont parallèles.
|
|
|
Questions-réponses : à quoi ça sert ?
- A quoi sert l’hypothèse « les points A, M et B d’une part, et les points A, N et C d’autre part sont alignés dans le même ordre » ? Quel est l’intérêt de la vérifier ?
Il permet de vérifier que les points sont bien positionnés comme dans une configuration de Thalès.
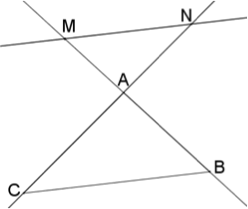
Sans cette hypothèse, on pourrait avoir des figures comme celle ci-dessous, où (MN) n’est clairement pas parallèle à (BC) alors que
AM
......
AB
est bien égal à
AN
......
AC
.
- Qu’est devenu le 3ème rapport du théorème de Thalès ? Le MN ...... BC ?
Il ne permet pas de montrer que les droites (MN) et (BC) sont parallèles.
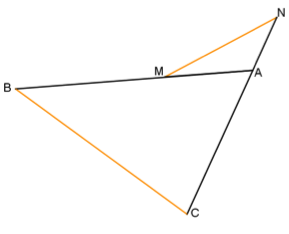
En fait, on peut tracer des figures comme celles de l’énoncé, où
MN
......
BC
=
AM
......
AB
mais où (MN) n’est pas parallèle à (BC).
Attention à ne pas le calculer en appliquant la réciproque !