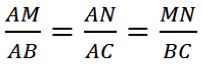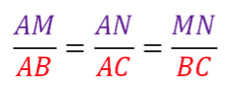Monsieur Thalès ?

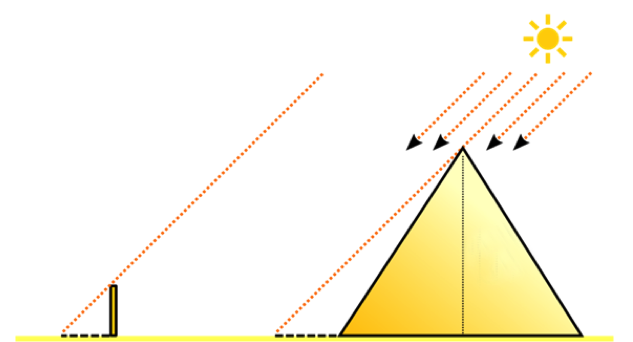
Né en -625 à Milet, dans l’actuelle Turquie, également commerçant, homme politique et philosophe, Thalès de Milet est, de par sa façon d’observer, d’analyser des situations et d’en recherches les causes,  l’un des précurseurs de la démarche scientifique moderne. Toutefois il ne reste aucun écrit de Thalès, même si on lui attribue de nombreux exploits comme la prédiction d’une éclipse, ou le calcul de la hauteur de la Grande Pyramide, réputée impossible à mesurer. 

Thalès aurait planté un bâton au sol et s’en serait servi, en mesurant l’ombre du bâton pour déterminer le moment de la journée où l’ombre de tout objet est égal à sa hauteur. Il suffit alors de mesurer la longueur de l’ombre de la pyramide pour en déduire la hauteur. Cela n’était possible que lorsque les rayons du soleil étaient perpendiculaires avec l’un des côtés de la pyramide, ce qui ne se produit que deux fois par an !

Thalès de Milet est le premier mathématicien à avoir laissé son nom dans l’histoire.

C’est en référence à cette histoire que le théorème étudié en 3^ème s’appelle théorème de Thalès, même si Thalès ne l’a pas lui-même démontré, et que son énoncé était sans doute déjà connu des Égyptiens. La démonstration de ce théorème n’a été donnée que trois siècles plus tard, par Euclide. Il existe en revanche d’autres propriétés formulées par Thalès, par exemple sur le cercle circonscrit à un triangle rectangle.

Le théorème de Thalès

Énoncé du théorème

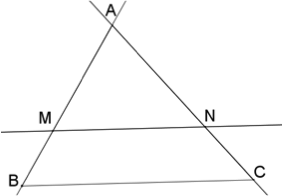
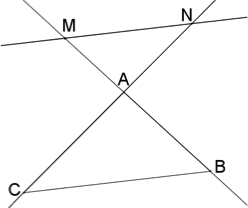
Soit un triangle ABC, et deux points M et N des droites (AB) et (AC) tels que la droite (MN) soit parallèle à la droite (BC). Alors : 

A quoi sert le théorème de Thalès ?

Ce théorème sert à calculer une longueur manquante dans des figures comportant un triangle et une droite parallèle à l’un des côtés.

On appelle d’ailleurs ces figures des configurations de Thalès.

Pour ne pas se tromper sur Thalès

Pour retenir l’égalité avec les trois fractions et savoir l’appliquer à d’autres triangles, on peut remarquer deux choses :

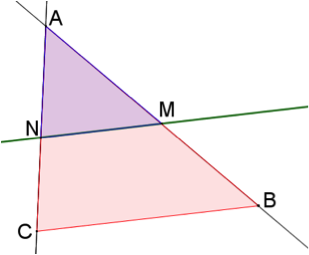
• Les longueurs des 3 numérateurs (ici, AM, AN et MN) font partie du même triangle AMN. Il en est de même pour les 3 dénominateurs (AB, AC et BC) qui font partie du triangle ABC.

Pour s’aider, on peut prendre l’habitude de placer les côtés du « petit » triangle au numérateur, et les côtés du « grand » triangle au dénominateur.

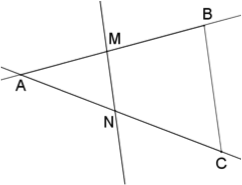
•  Les longueurs de deux fractions comportent toujours le point qui n’est PAS sur les droites parallèles (ici, le point A). 

De plus, dans ces deux fractions, le segment correspondant au numérateur est aligné avec celui du dénominateur ([AN] et [AC] sont alignés).

Comment utiliser le théorème de Thalès ?