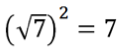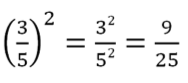Voici un cours très technique et assez abstrait pour des élèves de collège. Concentrons-nous ! 

Rappel de ce que votre enfant a appris avant 

En 5^ème et en 4^ème, on pratique le calcul littéral et la distributivité pour découvrir, par exemple, que :

Si un nombre multiplie une somme, comme dans un calcul de la forme k × (a + b)

On peut distribuer cette multiplication aux deux termes de la somme, 
ce qui donne k × a + k × b.

Cela s’appelle un développement, l’opération inverse s’appelle une factorisation.

Comme on peut enlever les signes ×, on écrit plutôt k(a + b) = ka + kb

De même, si on multiplie deux sommes, dans un calcul de la forme (a + b) × (c + d) 

On peut distribuer chaque terme de la première somme (a et b) à chaque terme de la deuxième somme (c et d), ce qui s’appelle un développement double, et donne a × c + a × d + b × c + b × d.

C’est plus facile à lire sans les signes × : 
(a + b)(c + d) = ac + ad + bc + bd

Les identités remarquables sont un cas particulier du développement double.

Ce sont trois égalités qui permettent de développer ou de factoriser certaines expressions plus simplement. Les voici :

(a + b)² = a² + 2ab + b²
(a – b)² = a² – 2ab + b²
(a + b) (a – b)  = a² – b²

Petit rappel : le ² signifie « carré ». 

Le carré d’un nombre est égal au nombre multiplié par lui-même.
 

Par exemple, 7² = 7 × 7 = 49, 
10² = 10 × 10 = 100, 
et (a + b)² signifie (a + b) × (a + b).

On peut démontrer que ces égalités sont vraies de plusieurs façons : en transformant (a + b)² en (a + b) (a + b) puis en développant, ou par un calcul d’aires de rectangles (si a et b sont positifs…).

Les identités remarquables sont à retenir par cœur pour savoir les utiliser dès que possible. Mais le plus important est de savoir s’en servir !

Savoir développer en 3ème

Développer signifie « passer d’un produit (une multiplication) à une somme (une addition) ».

Avec les identités remarquables, cela signifie, par exemple, passer de : 

• (a + b)² → a² + 2ab + b² ou encore de
• (a + b) (a – b)  →  a² – b²

Dans un exercice « classique », on est amené à développer, par exemple, (3x – 5)²

Comment faire ?

1. On recherche à quelle identité remarquable correspond cette expression, 
   parmi 
   (a + b)², (a – b)² ou (a + b)(a – b). 
   Ici, c’est (a – b)² !
2. On fait correspondre (3x – 5)² au a et au b de l’identité remarquable. 
   Ici, a vaut 3x et b vaut 5.
3. On applique la formule en remplaçant a et b. Comme (a – b)² = a² – 2ab + b², on écrit (3x – 5)² = (3x)² – 2 × 3x × 5 + 5²
   Attention : le a est remplacé par 3x, c’est donc 3x qu’il faut mettre au carré. Donc on ajoute des parenthèses autour de 3x, sinon seul le x serait mis au carré.
4. On effectue les multiplications et les mises au carré :
   (3x)² devient 3x × 3x = 9x²
   dans 2 × 3x × 5 on multiplie 2, 3 et 5 pour trouver 30, donc 2 × 3x × 5 = 30x
   et 5² = 5 × 5 = 25
   Finalement, (3x – 5)² = (3x)² – 2 × 3x × 5 + 5² =9x² – 30x + 25

Essayons encore avec (3 + 10x) (3 – 10x) 

1. On recherche à quelle identité remarquable correspond cette expression.
   Ici, c’est (a + b)(a – b).
2. On fait correspondre (3 + 10x) (3 – 10x) au a et au b de l’identité remarquable. 
   Ici, a vaut 3 et b vaut 10x.
3. On applique la formule en remplaçant a et b. 
   Comme (a + b) (a – b)  = a² – b²,
   on écrit (3 + 10x)(3 – 10x) = 3² – (10x)²
4. On effectue les multiplications et les mises au carré :
   (10x)² devient 10x × 10x = 100x²
   et 3² = 3 × 3 = 9
   Finalement, (3 + 10x)(3 – 10x) = 3² – (10x)²= 100x² – 9

Voilà pour les exercices les plus simples.

Attention aussi à deux erreurs fréquentes :

• Il ne faut utiliser les identités remarquables que quand c’est possible !

Par exemple, 2(3x – 5) ne comporte pas de carré, c’est un développement simple, 
et (3 – 4x)(5x + 3) ne comporte pas deux termes identiques dans les parenthèses, c’est donc un développement double, vu en 4^ème.

• (3x)² et 3x² ne signifient pas la même chose. 

Dans (3x)², le 3 et le x sont au carré, cela donne 9x² sans les parenthèses. Alors que dans 3x², seul le x est au carré, donc on ne modifie pas le 3.

Il faut aussi savoir combiner cette méthode avec les autres techniques de développement.

Par exemple, on peut développer 2(8x + 9)² qui demande d’utiliser une identité remarquable puis un développement simple.

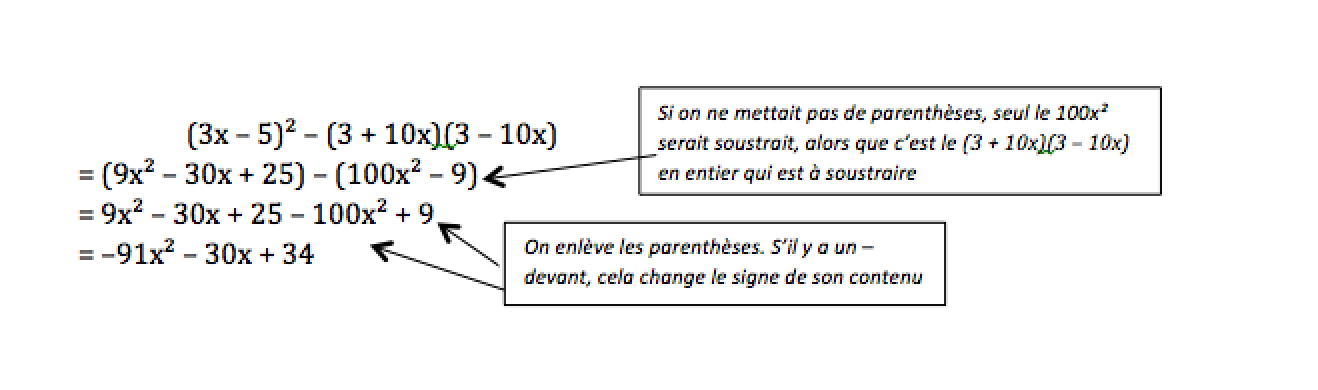
Ou encore (3x – 5)² – (3 + 10x)(3 – 10x) qui demande de calculer la différence des deux exemples précédents : 

 D’autres exercices peuvent aussi inclure :

• des racines carrées, il faut alors se rappeler que « la racine annule le carré » 

• des fractions, mais pour les mettre au carré, il suffit juste de mettre leur numérateur et leur dénominateur au carré

Apprendre à factoriser