Les premières traces de trigonométrie remontent au II^e siècle avant J.C. La paternité en est parfois attribué à Hipparque, mathématicien et astronome grec, qui s’en est servi notamment pour des calculs de distance entre le Soleil et la Terre, et qui a établi les premières tables trigonométriques.

Du grec : 
trígonos = « triangulaire »
métro = « mesure »

En 3^ème, on fait de la trigonométrie dans les triangles rectangles.

Petits rappels sur les triangles rectangles

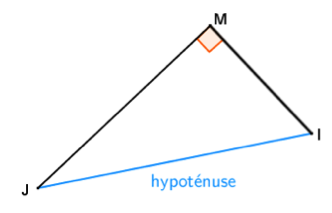
Un triangle rectangle, comme son nom l’indique, comporte un angle droit.

Le côté opposé à cet angle droit s’appelle hypoténuse. C’est le côté le plus long du triangle rectangle.

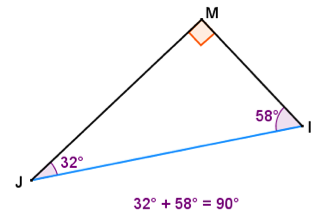
Puisque la somme des angles d’un triangle est de 180°, les deux autres angles d’un triangle rectangle sont aigus et la somme de leur mesure est 90°.

Par exemple, si un triangle rectangle comporte un angle de 32°, son autre angle aigu mesure 90 – 32 = 58°.

Enfin, deux définitions qui nous seront très utiles par la suite :

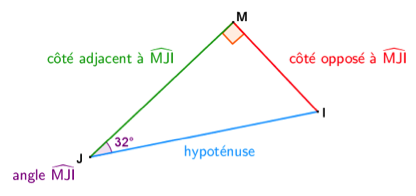
Étant donnés un triangle rectangle et un angle aigu :

• le côté adjacent à cet angle est le côté qui « touche » à la fois l’angle droit et l’angle aigu

(il existe bien un autre côté adjacent à l’angle, mais il porte déjà un nom : c’est l’hypoténuse)

• le côté opposé à cet angle est le côté qui ne « touche » pas l’angle aigu.

Les relations trigonométriques

Étant donnés un triangle rectangle et un angle aigu :

Le cosinus, le sinus et la tangente sont 3 nombres associés à cet angle, qui vont nous permettre :

• de calculer la mesure de cet angle, si on ne la connaît pas,
• de calculer une longueur manquante dans le triangle.

A chaque angle aigu correspond un cosinus, un sinus et une tangente.

Voici comment les calculer :