Mathématiques
La proportionnalité en 3ème
L’année de 3ème est l’occasion de consolider les connaissances sur la proportionnalité, et d’étudier des techniques plus efficaces pour calculer des augmentations ou des diminutions de pourcentage (ce qui s’avère bien pratique pour les soldes !)
Situations de proportionnalité
Pour rappel, deux grandeurs sont proportionnelles lorsque les valeurs de l'une s'obtiennent en multipliant par un même nombre non nul les valeurs de l'autre.
On appelle alors ce nombre le coefficient de proportionnalité et on les représenter dans un tableau de proportionnalité.
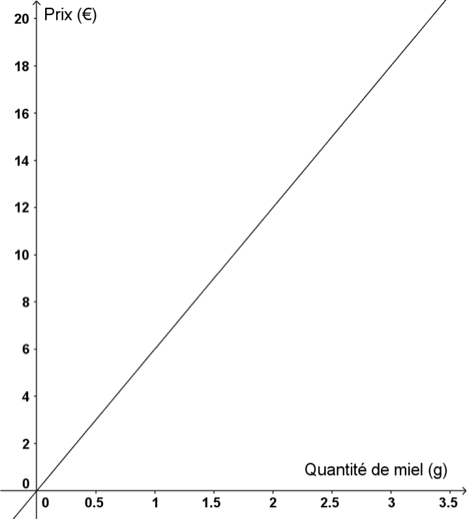
Deux grandeurs proportionnelles peuvent se représenter dans un graphique, sous la forme d’une droite alignée avec l’origine du repère.
Ce graphique correspond également à la fonction linéaire f : x → 6x .
Les fonctions affines et linéaires sont étudiées en 3ème.
Règle de trois
Dans la quasi-totalité des problèmes de proportionnalité, on cherche à trouver une valeur manquante, par exemple dans le problème suivant :
« Si trois kg d’oranges coûtent 5,7€, combien coûtent 5 kg d’oranges ? »
On dresse le tableau suivant :
On appelle la valeur recherchée la quatrième proportionnelle.
Plusieurs méthodes ont été vues au collège, mais la plus rapide, qui fonctionne toujours, et qui est très appliquée dans la vie courante, est la règle de trois.
On multiplie les deux valeurs connues disposées en diagonale, et on divise par la troisième.