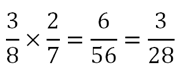Une urne et 1 000€

Imaginons un jeu télévisé avec une urne dans laquelle se trouvent 3 boules vertes et 5 boules rouges.

Un candidat doit tirer une boule, puis une autre, sans remise (entre les deux tirages, on ne remet pas la première boule tirée dans l’urne).  S’il tire deux boules vertes d’affilée, il gagne 1 000€.

Quelle est la probabilité que cela se produise ?

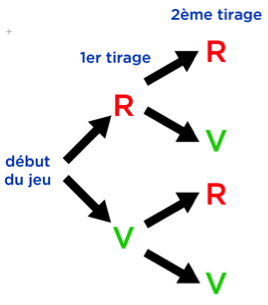
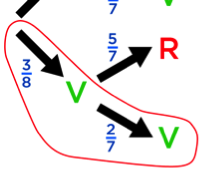
On peut représenter la situation par un arbre.

Chaque parcours représente une issue possible : on peut par exemple tirer une rouge puis une autre rouge, ou une verte puis une rouge, etc…
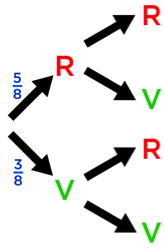
Ensuite, on complète cet arbre avec les probabilités de tirer une verte ou une rouge à chaque tirage.

Au premier tirage, c’est simple : la probabilité de tirer une rouge est de   5 .... 8   (il y a 5 boules rouges sur un total de 8) et celle de tirer une verte est de  3 .... 8 .

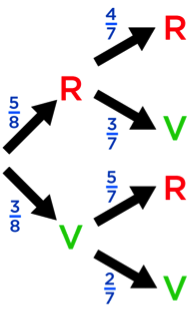
Ça se complique pour le deuxième tirage : comme ce jeu se fait sans remise, il ne reste que 7 boules dans l’urne.

Par exemple, si la première boule tirée était rouge, il reste 3 boules vertes et 4 boules rouges sur 7.
Et si la première boule tirée était verte, il reste 2 boules vertes et 5 boules rouges sur les 7.

Attention donc à cette difficulté, qui vient du fait qu’on étudie un tirage sans remise : si le tirage se faisait avec remise, ce serait plus simple, il suffirait de reprendre les probabilités du premier tirage.

 Voici l’arbre de probabilité au complet 

Répondons maintenant à la question du début : quelle est la probabilité d’empocher 1 000 € en tirant deux boules vertes d’affilée ?

Cela correspond au parcours « vert – vert » de l’arbre.

On calcule la probabilité de ce parcours en multipliant celles des deux « branches » qui le composent, c’est-à-dire :

Ce qui fait donc 3 chances sur 28 (environ 11 %) de remporter les 1 000 €. Pas si simple !

Et avec des dés…