Mathématiques au cycle 3
Grandeurs et mesures au cycle 3
Il s'agit d'aider les enfants à se construire progressivement des repères qui donnent du sens à chaque grandeur.
Les grandeurs étudiées au cycle 2 sont :
- la longueur (tu habites à 300 mètres de l’école) ;
- la masse (ton cartable ne doit pas peser plus de 3 kg) ;
- la contenance (c’est une bouteille d’eau d’1 litre et demi) ;
- la durée (il te faudra 3 heures 45 minutes pour aller voir ta grand-mère) et
- les prix (la baguette pour ton goûter coûte 1 euro 10 centimes).
Au cycle 3, les élèves ont déjà une bonne connaissance de la mesure des longueurs et poursuivent leurs apprentissages avec l’étude du périmètre d’une figure. La notion d’aire est aussi une nouveauté du cycle 3. Au cycle 3, les élèves apprennent également à comparer des angles ; l’utilisation du rapporteur pour exprimer une mesure en degrés est réservée à la 6ème. Ce n’est qu’en 6ème également que les élèves abordent la dernière nouveauté du domaine des Grandeurs et Mesures du cycle 3 : la notion de volume d’un solide (exprimé en m³), en lien avec la notion de contenance d’un récipient (c’est-à-dire le volume intérieur d’un récipient, exprimé en L).
Retrouvez nos fiches sur grandeurs et mesures par niveau CM1 et CM2.
Quelle est la démarche en classe ?
Pour chaque nouvelle grandeur, l’enjeu pour les élèves est de se construire des repères qui lui donnent du sens, en les rattachant au maximum à leur univers quotidien ou des situations vécues, en lien avec d’autres enseignements (le périmètre de la cour de récré, l’aire de la France, etc.).
Les élèves commencent par des activités de découverte (on compare, on estime ou on mesure à l’aide des instruments appropriés) avant la résolution de problèmes nécessitant des calculs et parfois des formules (formule du périmètre ou de l’aire d’un carré). Ils apprennent à manipuler les unités de mesure correspondantes, à utiliser le vocabulaire spécifique de cette grandeur et s’entraînent aux conversions et aux calculs. Un travail important de manipulation et d’estimation est donc réalisé qui permet aux enfants d’avoir une perception concrète de ces grandeurs et de leurs mesures.
Quelles que soient les unités de mesure, il est important de donner du sens à ces notions. Elles ne doivent pas rester des données abstraites ou inaccessibles. Il ne faut donc pas hésiter à les rattacher au quotidien de votre enfant, en l’incitant à les manipuler, par exemple à l’occasion de la préparation d’un gâteau, en faisant ranger par ordre croissant les produits de toilette de la salle de bain, etc.
Vous pouvez également lui proposer d’estimer des grandeurs de son environnement (sous forme de pari) avant qu’il n’aille en vérifier la mesure à l’aide d’instruments usuels.
Par exemple, dans la maison, suggérez-lui d’estimer l’épaisseur d’un dictionnaire, la hauteur de son bureau, la largeur d’une porte, la longueur de la voiture familiale, etc. en mettant à sa disposition un double-décimètre, un mètre de couturière, un décamètre d’architecte, etc.
Votre enfant va très vite se rendre compte que ces grandeurs sont utilisées quotidiennement dans la vie courante et qu’elles sont très utiles.
Ces petits défis sont pour votre enfant l’occasion de comprendre l’intérêt des multiples et sous-multiples et de se construire des représentations des unités les plus appropriées pour exprimer telle ou telle mesure.
S’il existe une unité légale pour chaque grandeur celle-ci n’est pas forcément la plus adaptée pour exprimer la mesure donnée (par exemple : on n’exprimera pas la distance entre Paris et New York en mètres, pas plus qu’on n’exprimera l’épaisseur d’un dictionnaire en mètres).
Pour exprimer une grandeur avec de plus précision, on peut utiliser d’autres unités :
- des sous-multiples de l’unité légale (par exemple : dm, cm et mm pour le mètre) ou
- des multiples (par exemple : dam, hm et km pour le mètre).
Les relations qui existent entre ces différentes unités sont définies par le système de la numération décimale (ou sexagésimale pour les durées).
Ainsi 1 m = 10 dm (le décimètre est dix fois plus petit que le mètre) et 1 dam = 10 m (le décamètre est dix fois plus grand que le mètre).
On peut procéder de même avec toutes les grandeurs étudiées (en utilisant différents types de balances pour les masses, différents types de contenants, bouteilles, verres-doseur pour les volumes, etc).
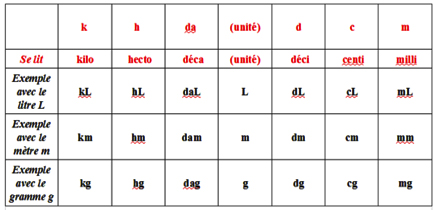
Tableau de conversion
Grâce à ce tableau de conversion, les élèves savent depuis le CE2 exprimer une même longueur dans différentes unités (exemple : 2 413 mm = 2 m 413 mm = 24 dm 13 mm = 241 cm 3 mm) ou à l’inverse, à exprimer une grandeur dans une seule unité (exemple : 3 km et 45 m = 3 045 m).
Ils sont également capables de comparer des grandeurs et de les ordonner (exemple : ranger par ordre croissant / décroissant).
Ces problèmes utilisent des nombres entiers de plus en plus grands et des nombres décimaux, puisque grâce à leurs connaissances sur les nombres, les élèves savent exprimer une grandeur sous la forme d’un nombre décimal ( par exemple : 1 m et 45 cm = 1 unité et 45 centièmes = 1,45 m).
Les élèves consolident ainsi leurs apprentissages des nombres décimaux et sont capables d’établir le lien entre les unités de numération et les unités de mesure :
- dixième / dm/ dL / dg ;
- centième/cm / cL / cg ; etc.
Ils savent également utiliser les fractions décimales pour exprimer une mesure.
Par exemple : 1hm = 100 m donc 1 m = 1 ........ 100 hm = 0,01 m
Ou 1 dL = 1/10 L = 0,1 L
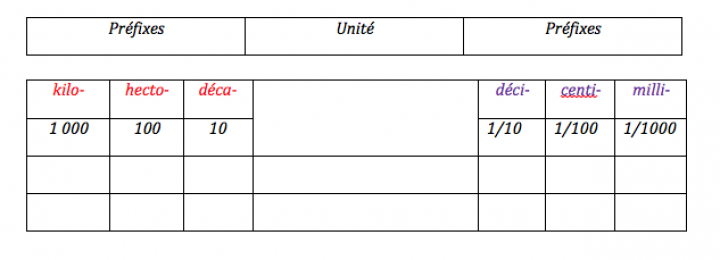
1 décamètre =10 mètres
1 hectomètre =100 mètres
1 kilomètre =1000 mètres
1 décimètre = 1 ...... 10 mètre
1 centimètre = 1 ........ 100 mètre
1 millimètre = 1 .......... 1000 mètre
La proportionnalité
Enfin, les élèves apprennent à reconnaître une situation de proportionnalité entre deux grandeurs. Pour donner du sens à ces nouveaux apprentissages, les situations problèmes impliquant la proportionnalité, sont progressivement choisies en lien avec d’autres disciplines : des problèmes d’échelle en géographie (lecture de cartes), de vitesse en éducation physique et sportive, de calculs de pourcentages en sciences ou en histoire.
Des exemples de problèmes avec les grandeurs
Faire le plan de l’école
Les élèves doivent mesurer les grandeurs réelles des principaux espaces, trouver ensuite une échelle convenable pour les représenter sur un plan, et enfin calculer les longueurs du plan par proportionnalité.
Un calcul d’échelle
Un directeur dispose du plan du gymnase de son école, représenté à l’échelle 1/100. Remplissez le tableau avec les dimensions réelles du gymnase :
| Longueur | Largeur | |
| Dimensions sur le plan (en cm) | ||
| Dimensions réelles (en cm) |
Le directeur souhaiterait pouvoir délimiter au sol du gymnase, le périmètre d’un terrain de basketball mesurant 28 m de long et 15 m de large. Quelles sont les dimensions de ce terrain à l’échelle 1/100 ? Représentez-le sur le plan.
Calcul de superficie
La région Normandie a une superficie de 29 906 km². Depuis le 1er janvier 2016, elle est composée de l’ancienne région Basse-Normandie qui a pour superficie 17 589 km² et de l’ancienne région Haute-Normandie. Quelle est la superficie de la Haute-Normandie en km² ? Et en m² ?