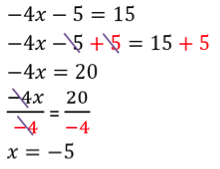Fonction affine ?

Une fonction affine est de la forme f : x → ax + b ou bien f(x) = ax + b, 
a et b étant deux nombres

a s'appelle le coefficient directeur et 
b l’ordonnée à l’origine (nous verrons pourquoi dans quelques paragraphes !). 

Un exemple

la fonction g(x) = -3x + 5 est affine : 
le coefficient directeur (a) vaut – 3 et l’ordonnée à l’origine (b) vaut 5.

Le calcul d’une image par g peut se représenter par la « machine mathématique » ci-dessous :

Ainsi, l’image de 4 par cette fonction est g(4) = -3 × 4 + 5 = – 12 + 5 = – 7.

Toutes les fonctions affines reviennent à faire les mêmes opérations : en partant du nombre de départ, on le multiplie par le coefficient directeur, puis on lui ajoute l’ordonnée à l’origine.

Ces deux nombres peuvent être négatifs, donc il faut parfois soustraire au lieu d’ajouter.

Quelques exemples de fonctions affines

• f(x) = 4x – 7

Le coefficient directeur est 4, l’ordonnée à l’origine est – 7.

• f(x) =  3 .... 2  x + 5  

Le coefficient directeur est  3 .... 2  , l’ordonnée à l’origine est 5.

• f(x) = 9x

Le coefficient directeur est 9, il n’y a pas d’ordonnée à l’origine, qui est donc égale à 0. 
On appelle cela une fonction linéaire.

• f(x) = 8,5

Il n’y a pas de coefficient directeur, qui est donc 0. L’ordonnée à l’origine est 8,5. C’est une fonction constante.

Pour ne pas se tromper

Le coefficient directeur est le nombre qui multiplie x, 
l’ordonnée à l’origine est le nombre qui est ajouté ou soustrait.

Calcul d’image

Il est assez facile de calculer l’image d’un nombre par une fonction affine.
Par exemple, pour la fonction g(x) = -4x – 5, si on souhaite calculer l’image de -2, il suffit de remplacer x par -2 :

g(-2) 
= -4 × (- 2) – 5 
= 8 – 5 
= 3. 

L’image de -2 par g est 3. Cela peut se représenter par le schéma ci-dessous :

Calcul d’antécédent

Il est plus difficile de calculer un antécédent, c’est-à-dire de retrouver un « nombre de départ » quand on connaît le « nombre d’arrivée ».

Par exemple, calculons un antécédent de 15 par la fonction g(x) = -4x – 5 :

Cela ne revient pas à remplacer x par 15, ce qui nous donnerait non pas un antécédent mais l’image de 15.

Pour calculer un antécédent, il faut chercher le nombre x tel que g(x) = 15.
Autrement dit, comme g(x) = -4x – 5, on résout l’équation -4x – 5 = 15.

On trouve que l’antécédent de 15 par la fonction g est – 5.

En résumé : pour trouver l’antécédent d’un nombre y par une fonction affine f(x) = ax + b, il suffit de résoudre l’équation ax + b = y.

Représentation graphique