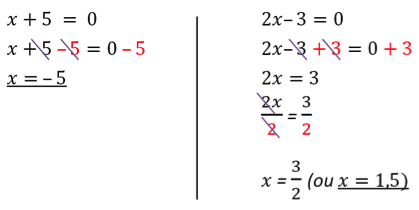Ce chapitre permet de voir des techniques pour résoudre des équations un peu plus complexes, notamment en utilisant la factorisation et les identités remarquables. Ces techniques seront encore améliorées en 2^nde et en 1^ère.

Une règle importante

Commençons par une règle à la fois évidente et très importante ici :

« Un produit est nul, si et seulement si l’un des facteurs est nul »

En effet :

• Lorsqu’on multiplie 0 par n’importe quel nombre, on trouve toujours 0.
• Si lors d’une multiplication on trouve 0, cela signifie que l’un des deux nombres multipliés (les facteurs) était égal à 0.

On peut l’écrire de façon plus synthétique : « A × B = 0 signifie que A = 0 ou que B = 0 ».

Cette règle est à rappeler à chaque fois qu’on doit résoudre une équation produit nul.

Les équations produit nul

Ce sont des équations dont le premier membre est un produit (une multiplication) et l’autre membre est zéro.

Par exemple, l’équation (x + 5)(2x – 3) = 0 est une équation produit nul :

• Le membre de droite est zéro,
• Le membre de gauche est un produit : n’oublions pas qu’entre deux parenthèses « collées » se cache une multiplication !

On pourrait réécrire cette équation en faisant réapparaître la multiplication : (x + 5) × (2x – 3) = 0.

Voici d’autres exemples d’équation produit nul :

• (3x – 4)(7 + 0,5x) = 0
• 2y(5 + 8y) = 0
• 0 = (8x + 3)( 4 .... 5 x + 7)

Notez qu’à chaque fois, le produit est « sous-entendu » : on n’écrit pas le signe × avant une parenthèse.

Et voici quelques équations qui ne sont PAS des équations produit nul :

• 3(5x + 4) + 7x = 0

Le membre de gauche n’est pas un produit, mais une somme.

• 2t(9t - t) = 11

Aucun membre n’est égal à zéro.

• 49x² + 9 = 42x

Tout faux ! Le membre de gauche est une somme, le membre de droite n’est pas zéro… mais nous verrons quand même une technique pour « transformer » cette équation en équation produit nul !

Comment résoudre une équation produit nul ?

 Repartons de l’équation (x + 5)(2x – 3) = 0

Pour la résoudre, on pourrait être tenté de développer ce produit, comme cela a été vu en 4^ème :
(x + 5)(2x – 3) = x × 2x – x × 3 + 5 × 2x – 5 × 3 = 2x² – 3x + 10x – 15 = 2x² + 7x – 15 
L’équation devient donc 2x² + 7x – 15 = 0, mais nous ne sommes pas plus avancés qu’avant !

Les techniques enseignées en 4^ème ne permettent pas de résoudre les équations comportant une inconnue x et son carré x².

Il faut plutôt utiliser la propriété vue précédemment :

« Un produit est nul, si et seulement si l’un des facteurs est nul »

Nous avons bien affaire à un produit nul : (x + 5) × (2x – 3) est égal à zéro.
Ainsi, cela signifie que soit x + 5 = 0, soit 2x – 3 = 0.
Donc plutôt que de résoudre l’équation (x + 5) × (2x – 3) = 0 en une fois, on peut la décomposer en deux équations très simples :

• x + 5 = 0 et
• 2x – 3 = 0 que l’on va résoudre séparément, avec les techniques vues en 4^ème.

Voici la solution rédigée :

On résout l’équation (x + 5)(2x – 3) = 0
Un produit est nul, si et seulement si l’un des facteurs est nul. 
Ainsi :

 L’équation (x + 5)(2x – 3) = 0 admet deux solutions : – 5 et  3 .... 2  (ou 1,5)

 Un peu plus difficile : l’équation  – 4x(7x –  3 .... 4  ) = 0

 Un produit est nul, si et seulement si l’un des facteurs est nul. 
Ainsi :

L’équation – 4x(7x – 3 .... 4  ) = 0 admet deux solutions : 0 et  3 ...... 28  (qui n’a pas d’écriture décimale)

Factorisation et identités remarquables

Parfois, il est nécessaire de « transformer » une équation pour pouvoir la résoudre avec cette méthode. Il est même parfois nécessaire d’utiliser les identités remarquables.

Une première factorisation