Mathématiques
Nombres et calculs au CM2
L’objectif du domaine Nombres et calculs est que votre enfant soit capable de résoudre des problèmes mathématiques utilisant des nombres entiers, des nombres décimaux ou des fractions simples, grâce à ses connaissances en calculs.
Pour y parvenir, trois activités sont combinées tout au long du CM2 :
- l’étude des nombres (entiers, fractions simples et nombres décimaux),
- l’entraînement aux calculs (mental, posé, en ligne ou avec calculatrice) et
- l’entraînement à la résolution de problèmes.
L’étude des nombres
En arrivant au CM2, votre enfant a déjà une bonne connaissance des grands nombres entiers (jusqu’au million) et des nombres décimaux, découverts au CM1. N'hésitez pas à vous reporter à la fiche Nombres au CM1 pour y retrouver en détails la progressivité des ces apprentissages.
L’objectif du CM2 est d’approfondir et de structurer ces connaissances.
Les nombres entiers
Depuis le CM1, votre connaît les nombres entiers jusqu’à million : il est capable de les lire et de les écrire (en chiffres et en lettres), de comparer et de les ranger. L’objectif de la fin du cycle 3 est le milliard, et certains enseignants commencent dès le CM2 à initier leurs élèves à ces très grands nombres.
Au CM2, votre enfant doit parfaitement maîtriser les relations qui existent entre les différentes unités de numérations des entiers :
- les unités simples,
- les dizaines et
- les centaines de chaque ordre.
Les fractions et les nombres décimaux
C’est au CM1 que votre enfant a découvert les fractions décimales et les nombres décimaux, très utiles pour mesurer ou partager des grandeurs qui ne sont pas entières (voir la fiche Nombres au CM1.
Au CM2, votre enfant approfondit ses connaissances sur les fractions : il est capable de les lire, de les écrire et de les représenter sans hésitation sur une droite graduée.
Il est aussi capable d’écrire une fraction sous forme d’un nombre entier et d’une fraction inférieure à 1.
Par exemple : 15/4 = 4/4 + 4/4 + 4/4 + ¾ = 1 + 1 + 1 + ¾ = 3 + ¾
Il sait que 3 représente la partie entière et ¾, la partie fractionnaire (fraction inférieure à 1)
Votre enfant sait également qu’une fraction décimale peut s’écrire sous la forme d’un nombre décimal.
Par exemple :
65 ...... 10 = 6,5
65 ........ 100 = 0,65
65 452 ........................ 1 000 = 65,452
Enfin, votre enfant approfondit ses compétences sur les nombres décimaux : il est capable de plus en plus facilement de les comparer et les ranger.
N’hésitez pas à l’entraîner à retenir quelques fractions usuelles et leur équivalence avec virgule :
½ (un demi) = 0,5
1/5 (un cinquième) = 0,20
1/4 (un quart) = 0,25
¾ = 75/100 =0,75
1/10 (un dixième) = 0,1
1/100 (un centième) = 0,01
L'entraînement au calcul
Rappelons qu’au cycle 3, votre enfant s’entraîne à quatre types de calcul : calcul mental, calcul en ligne, calcul posé, calcul avec calculatrice.
En début de cycle 3, les élèves ne perçoivent pas forcément l’intérêt de ces apprentissages qui leur paraissent fastidieux ; ils sont pourtant la base de tous les autres calculs!
Prenons l’exemple de la technique opératoire de la division, qui demande à la fois des connaissances sur les tables de multiplication et de soustraction…Si les tables ne sont pas parfaitement sues, les enfants ne pourront pas effectuer de division.
Retrouvez en détails la progressivité de ces apprentissages dans notre fiche Le calcul au CM1.
Calcul mental et calcul en ligne
Au CM2, votre enfant poursuit en classe son entraînement au calcul mental et au calcul en ligne, en suivant la progression de ses apprentissages en nombres et en opérations.
Par exemple, dès qu’il a appris à poser la multiplication d’un nombre décimal par un nombre entier, votre enfant peut être entraîné à multiplier mentalement des entiers et des décimaux
(par exemple : 38,8 x 100).
Pas un jour sans calcul mental ! N’hésitez pas à l’entraîner en téléchargeant des applis spécialisées en calcul mental, comme Mathador (gratuit) ou CapMaths (Hatier, payant).
Défiez-le et chronométrez-le !
Ces rituels ainsi organisés à la maison ont montré toute leur efficacité dans l’automatisation et la vitesse de réaction du calcul mental, et ont surtout permis de réconcilier plus d’un enfant avec le calcul mental !
D'ailleurs une nouvelle circulaire du ministre de l'Education Nationale demande aux enseignants, à partir de la rentrée 2018, d'organiser des séances quotidiennes de 15 minutes de calcul mental, en variant les supports : ardoise, cahier d'entraînement, à l'oral, au tableau de la classe, etc.
Le calcul posé est un calcul posé en colonnes, que votre enfant apprend en classe suivant une technique enseignée par son professeur.
Le calcul posé
En arrivant au CM2, votre enfant connaît déjà toutes les techniques opératoires : l’addition, la soustraction, la multiplication et la division.
Au CM1, il a appris à additionner et soustraire des nombres décimaux ; au CM2, il apprend la multiplication d’un nombre décimal par un nombre entier.
La première étape, c'est de poser la multiplication sans tenir compte de la virgule et de calculer.
Puis, votre enfant apprend qu'il faut compter le nombre de chiffres après la virgule du nombre décimal pour ensuite venir placer une virgule dans le résultat afin qu'il y ait autant de chiffres après celle-ci que dans le nombre décimal de départ.
Prenons un exemple : 2,41 x 3
On place donc la virgule juste après le 7 du résultat.
N'hésitez pas à visionner les petites vidéos très ludiques du site Canopé (Education Nationale) pour aider votre enfant à visualiser et comprendre autrement ce mécanisme opératoire de la multiplication d'un décimal par un entier.
Au CM1, votre enfant a également découvert la technique opératoire de la division euclidienne (division de deux nombres entiers dont le résultat est un nombre entier, par exemple : 208 : 8 = 26).
Au CM2, il approfondit ses compétences en division et apprend à diviser de deux nombres entiers avec quotient décimal.
Qu’est-ce qu’un quotient décimal ?
Quand on effectue une division et qu’il y a un reste, on peut continuer la division pour avoir un résultat plus précis. On obtient un quotient décimal.
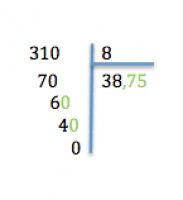
Par exemple
310 ÷ 8
On calcule la partie entière du quotient : 310 divisé par 8 = 38 il reste 6.
On place alors une virgule après la partie entière du quotient : « 38, »
Puis on calcule la partie décimale du quotient en écrivant un 0 à la droite du reste (certains disent « en abaissant un 0 » et on continue l’opération.
310 ÷ 8 = 38,75 reste 0.
Au CM2, on peut calculer la division au dixième près (c’est-à-dire un chiffre après la virgule) ou au centième près (deux chiffres après la virgule).
Au CM2, votre enfant apprend également à diviser un nombre décimal par un nombre entier.
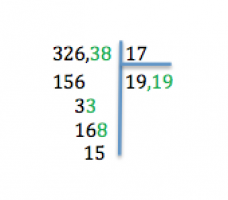
Par exemple
326,28 ÷ 17
On divise d’abord la partie entière du dividende par le diviseur :
326 ÷ 17 = 19 reste 3
On place ensuite la virgule du quotient (19,) et on abaisse le chiffre des dixièmes : 3
33 ÷ 17 = 1 reste 6
On abaisse alors le chiffre des centièmes : 8
168 ÷ 17 = 9 reste 15.
Pour vérifier si le résultat est juste, on multiplie e quotient par le diviseur et on ajoute le reste :
(19,9 x 17) + 0,15
Retrouvez plus de détails et d'exemples dans nos fiches :
Au CM2, l’utilisation de la calculatrice est introduite en lien avec le calcul mental et le calcul posé et la résolution de problèmes. Par exemple, la calculatrice permet à votre enfant d’effectuer rapidement certains calculs pour qu’il se concentre sur la compréhension et la résolution de problèmes. Elle permet également de jouer avec les grands nombres, de vérifier un résultat.
Le tableau ci-dessous rappelle les compétences de calcul acquises au CM1 et à consolider au cours du CM2. Il donne aussi les compétences de calcul à acquérir au cours de l’année de CM2
| Compétences | CM1 | CM2 |
|---|---|---|
| Calculer mentalement |
|
diviser un nombre entier ou décimal par 10, 100 ou 1000 |
| Effectuer un calcul posé |
|
|
| Utiliser une calculatrice | connaître quelques fonctionnalités utiles pour effectuer une suite de calculs | utiliser sa calculatrice à bon escient |
| Résoudre des problèmes | engageant une démarche à une ou plusieurs étapes |
L’entraînement à la résolution de problèmes
Au CM2, les problèmes proposés à votre enfant deviennent de plus en plus complexes en faisant évoluer :
- les nombres utilisés : les nombres entiers et les nombres décimaux sont de plus en plus grands,
- les calculs à effectuer : les problèmes relèvent des quatre opérations, l’objectif est d’automatiser la reconnaissance de l’opération attendue (situations additive, soustractive, multiplicative ou de division),
- le nombre des étapes de calcul : les problèmes peuvent nécessiter plusieurs étapes de calcul avant de parvenir au résultat final amis les questions intermédiaires peuvent être écrites dans l’énoncé.
- la forme des énoncés : les informations utiles pour résoudre un problème ne se trouvent que dans un seul type d’énoncé à la fois : un texte, un tableau ou un graphique.
L’entraînement à la lecture puis à la construction de nouvelles représentations est organisé se poursuit au CM2 : tableaux (simples ou à double entrée), graphiques en courbes, puis diagrammes en bâtons, circulaires (camemberts) ou semi-circulaires. Vous pouvez consulter la fiche Nombres et calculs au cycle 3.
Au CM2, votre enfant est également entraîné à résoudre des problèmes relevant de la proportionnalité, d’abord avec des nombres entiers puis des nombres décimaux (par exemple : « si j’ai deux fois, trois fois… plus d’invités, il me faudra deux fois, trois fois… plus d’ingrédients »).
Le sens de l’expression « …% de » n’apparaît qu’en milieu de cycle, et les calculs avec un taux de pourcentage ne sont introduits qu’en 6ème.
Quel que soit le type de problème, votre enfant doit être capable d’expliquer son raisonnement à l’oral comme à l’écrit. Depuis le CM1, il apprend progressivement à rédiger sa démarche et à présenter ses résultats.
« Je suis nul en problèmes ! ».
Combien de fois ai-je entendu cette réflexion de la part de mes élèves, ou pire, de leurs parents ?
« Etre nul en problèmes », cela n’existe pas !
A partir du diagnostic de l’erreur commise, l’enseignant a la possibilité de cerner la difficulté rencontrée par un élève pour l’aider à y remédier. Vous trouverez ici des listes d'erreur et des moyens pour les corriger ainsi que la présentation souhaitée d'un problème au CM2.