Mathématiques
Médiatrice et symétrie axiale en 6ème
Il existe 2 types de symétrie (par rapport à un point ou une droite). En 6ème on étudie uniquement la symétrie par rapport à une droite (= un axe), on parle donc de symétrie axiale.
Pour comprendre la symétrie axiale il faut d’abord comprendre la notion de médiatrice.
C'est quoi une médiatrice ?
La médiatrice est une droite.
On parle de médiatrice d’un segment, pas question donc de parler de médiatrice sans y associer un segment.
La médiatrice d’un segment est la droite qui coupe perpendiculairement ce segment en son milieu.
Un exemple pour mieux comprendre
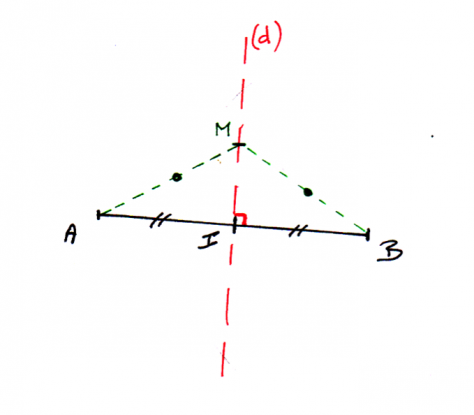
Soit un segment [AB] et I son milieu. (d) est la médiatrice du segment [AB] :
- (d) ⟘ (AB)
- I ∈ (d)
Soit M un point de (d) alors MA = MB et les droites (MI) et (d) sont confondues.
On obtient alors les 2 propriétés caractéristiques de la médiatrice :
- Propriété : Si un point appartient à la médiatrice d’un segment alors il est équidistant des extrémités de ce segment.
- Propriété : Si un point est équidistant des extrémités d’un segment alors ce point appartient à la médiatrice de ce segment
Dans un triangle la médiatrice est considérée comme une des 4 droites particulières (les 3 autres sont la médiane, la bissectrice et la hauteur). Ces droites particulières ont des propriétés particulières.
Propriété particulière des 3 médiatrices d’un triangle
Dans un triangle il y a 3 côtés donc 3 segments donc 3 médiatrices.
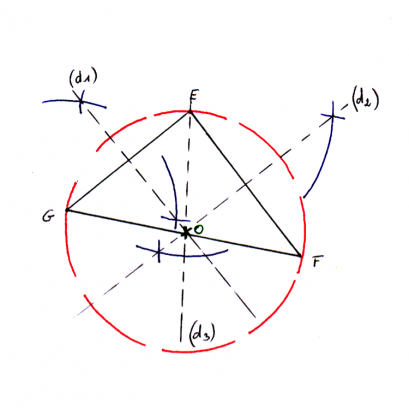
Les 3 médiatrices d’un triangle, par propriété, sont concourantes (elles se coupent en 1 point unique). Ce point est appelé centre du cercle circonscrit au triangle.
On dit encore que le triangle EGF est inscrit dans le cercle de centre O et de rayon OG=OE=OF avec O point de concours des 3 médiatrices du triangle EGF.
Pour construire une médiatrice
Pour construire la médiatrice d’un segment il faut une équerre ou un compas et une règle.
Construction de la médiatrice d’un segment [AB].
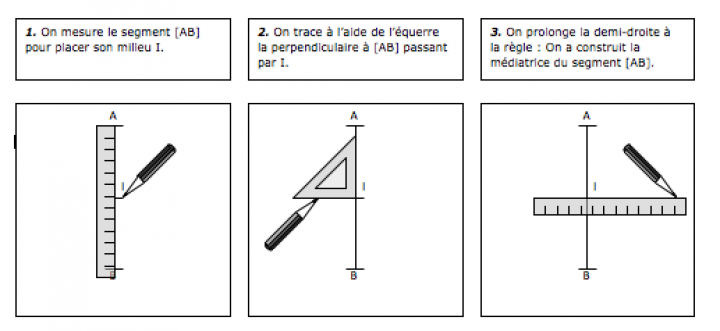
Avec la règle et l’équerre
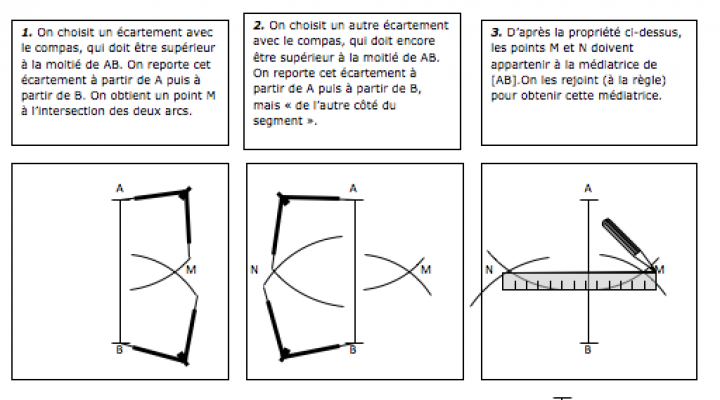
Avec un compas
Attention
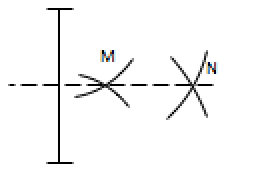
Dans certains cas, on peut être amené à placer les points M et N du même côté du segment [AB] (par exemple quand le segment [AB] se trouve très près du bord de la feuille).
Il faut alors s’efforcer d’avoir des points M et N le plus éloignés possible, ce qui rendra la construction plus précise.