Mathématiques
Le cercle en 6ème
Un cercle est un ensemble de points situés à la même distance (rayon du cercle) d’un unique point, appelé centre du cercle.
Par exemple, prenez un lacet que vous tendez et fixez une des extrémités dans le sable. A partir de l’autre extrémité tracez au sol, tout en tournant autour de la 1ere extrémité, une trace dans le sable. On obtient alors un joli cercle sur la plage qui nous permettra de délimiter alors les fortifications autour de notre château que l’on placera à l’emplacement du centre.
Soit le cercle (ℰ) de centre O
Soit le cercle (ℰ) de centre O et passant par B.
On parle alors du cercle (ℰ) de centre O et de rayon r=OB (distance entre les points O et B).
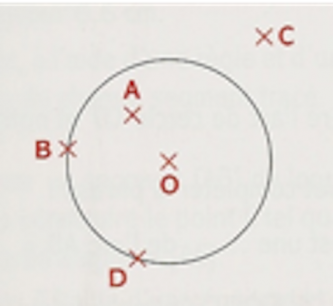
Sur la figure ci-dessous B et D sont des points de (ℰ), A est un point du disque(Δ) de centre O et de rayon r et le point C n’appartient ni au cercle ni au disque.
On notera :
- B ∈ (ℰ) = B appartient au cercle (ℰ)
- D ∈ (ℰ) = D appartient au cercle (ℰ)
- A ∈ (Δ) = A appartient au disque (Δ)
- C ∉ (ℰ) = C n'appartient pas au cercle (ℰ)
- C ∉ (Δ) = C n'appartient pas au disque (Δ)
Attention aux notions Différentes : il faut distinguer la notion de rayon (mesure) et la notion de rayon (segment).
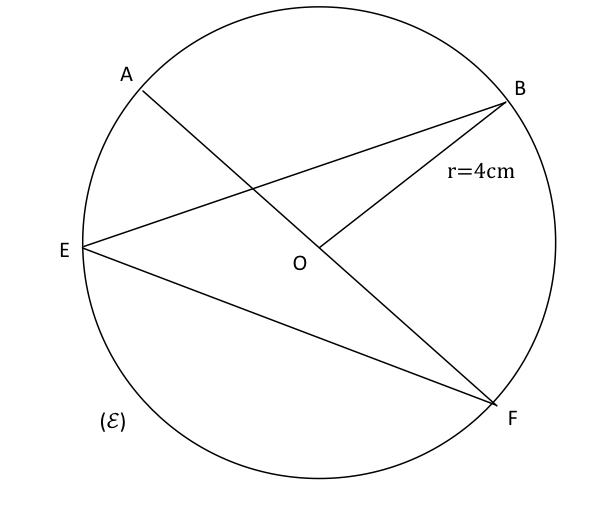
Dans le cercle (ℰ) ci-dessous
Mesure : (ℰ) est le cercle de centre O et de rayon (mesure) 4 cm avec OA=OB=OE=OF=r= 4 cm.
Segment : Les points A, B, E et F sont des points de (ℰ) donc les segments [OA], [OB], [OE], [OF] sont des rayons (segments) de (ℰ).
Un peu de vocabulaire :
A et F sont 2 points du cercle (ℰ) tels que : A, F et O(le centre) alignés.
[AF] est donc un diamètre de (ℰ) et AF=2xr.
[EF] est une corde de (ℰ) car E, O, et F ne sont pas alignés
B est un autre point du cercle donc [EB] est aussi une corde.
Une remarque :
[OB] n’est pas corde car O ∉ (ℰ)