La « figure » triangle est importante, car elle relie la notion de distance entre 2 points et la notion de l'angle entre 2 directions. Mais elle permet également de visualiser aisément la notion de chemin le plus court entre 2 points. Grâce à elle on peut facilement faire le lien entre « le monde mathématique » et des situations de la vie réelle.

L’objectif de cette fiche et de vous montrer des constructions « qui collent » à la réalité tout en vous donnant les clefs pour les construire.

N’hésitez pas à consulter les fiches « Angles » et « Aires et Périmètres » qui vous donneront d’autres précisions sur les « grandeurs » liées à la « figure » triangle.

Qu’est-ce qu’un triangle ?

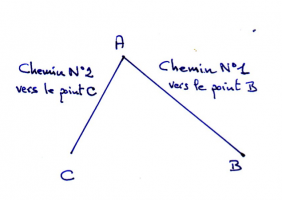
Un angle est 1 point (appelé sommet) dont partent 2 chemins (les côtés de l’angle). 

A est le point de départ des 2 chemins. A est appelé le sommet de l’angle BÂC. 
On obtient alors le triangle ABC avec

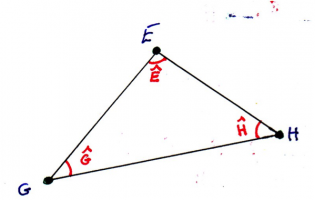
Le triangle EGH a 

• 3 sommets E, G, H
• 3 angles Ê, Ĝ, Ĥ
• 3 côtés [EH], [EG], [HG]

  

Comment construire un triangle ?

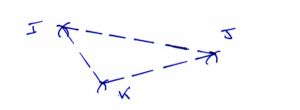
Qui dit point dit crayon                  

En plaçant 3 points I, J, K avec son crayon, et en les reliant, on a construit un triangle. 

Qui dit angle dit rapporteur

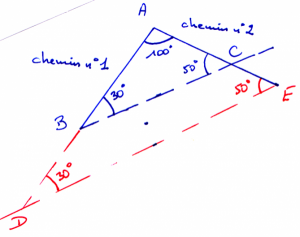
On peut construire 2 triangles différents (ou plus encore) avec les mêmes 3 angles : 

            ABC et ADE ont respectivement les mêmes 3 angles 100°, 30° et 50°. 

« lien à faire vers la fiche angle »

A partir du point A (sommet d’angle 100°), on peut placer son rapporteur n’importe où sur le chemin numéro 1 ou numéro 2 et construire un angle de 30° ou 50°.

On obtiendra alors différents triangles dont la définition « angulaire » est la même : 100°, 30°, 50°.

Qui dit coté dit longueur dit règle ou compas  

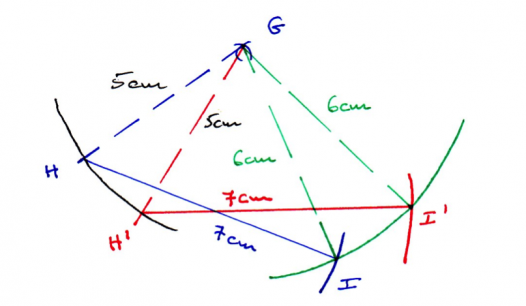
Les triangles GHI et GH’I’ sont caractérisés tous les 2 par les mêmes longueurs : 5cm, 6cm, 7cm. 

Méthode pour tracer un triangle au compas

1. On trace un arc de cercle de centre G et de rayon 5cm. Sur cet arc de cercle on place 2 points (ou plus), nommés ici H et H’.
2. On trace un arc de cercle de centre G et de rayon 6cm.
3. A partir de H ou H’ (ou des autres points placés à l’étape 1), on trace un arc de cercle de rayon 7cm.
4. L’intersection des arcs de cercle tracés à l’étape 1 et 3 donne le point I ou I’.

Conseils pour les constructions triangulaires

3 cas de figure déterminent un triangle unique:

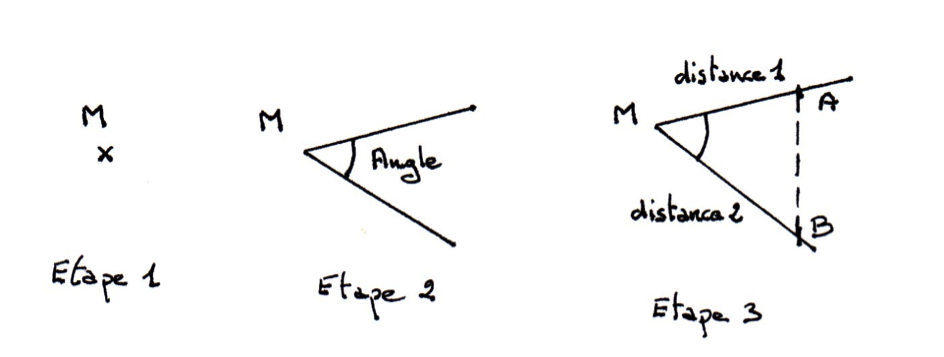
1 angle et 2 distances

On part du sommet de l’angle « tracé lui-même à l’aide du rapporteur » et on construit les « 2 distances » : 

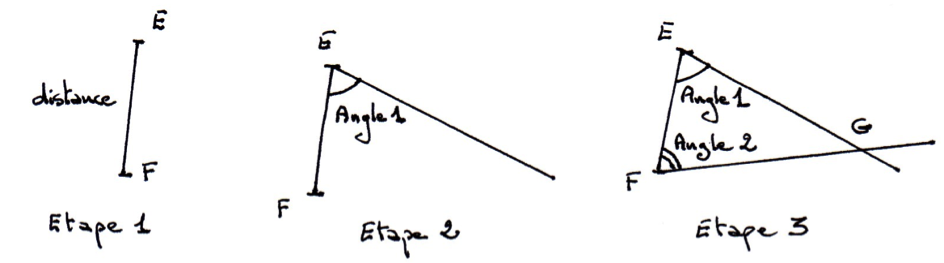
2 angles et 1 distance 

On trace un segment de la distance donnée. 
A partir des 2 extrémités du segment, on trace « à l’aide du rapporteur » les 2 angles donnés : 

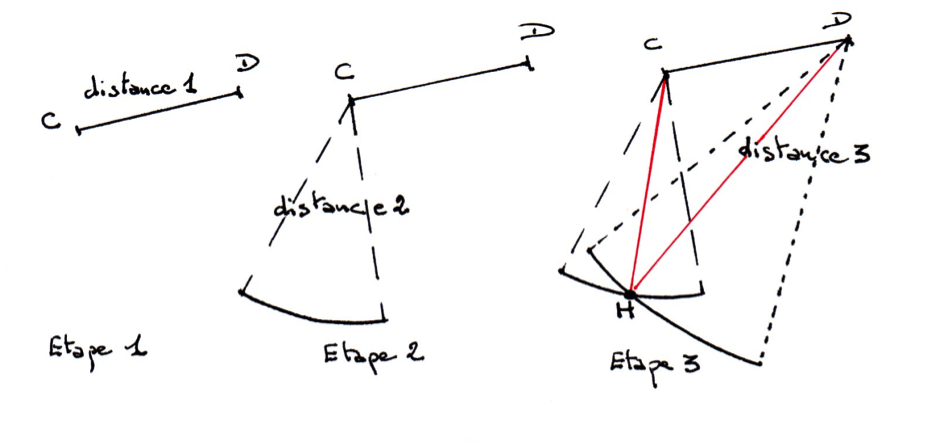
3 distances

On trace les 3 segments dont les 3 distances sont données, à la « queue le le »: 

• 1ère étape: on trace un des trois côtés à la règle = distance 1.
• 2ème étape: avec le compas, on trace un arc de cercle à la distance 2 voulue en partant d'une des extrémités du segment. 
• 3ème étape: on recommence de l'autre côté du segment avec la distance 3.
• 4ème étape: le point d'intersection obtenu donne le 3ème sommet. Ne reste plus qu'à le relier (en rouge ici!).

Si on donne à votre enfant les 3 longueurs du triangle, il doit utiliser la règle et son compas. 

Comme on l'a vu, 3 angles ne définissent pas un triangle unique mais des triangles dont les cotés seront portés par les mêmes directions.

Vos outils « amis » sont le compas et la règle graduée. Mais si je ne devais en choisir qu’un seul, mon meilleur ami serait le compas car il est le plus précis pour reporter des distances (même inconnues).

Des triangles particuliers 

Le triangle isocèle 

Le mot isocèle vient du grec et signifie "ayant deux jambes égales". Un triangle isocèle a donc deux côtés de même longueur. 

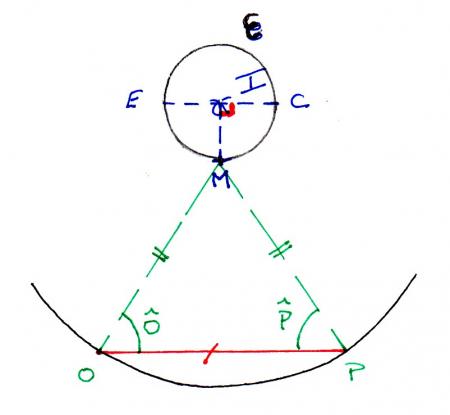
Le chapeau du clown 

On trace le chapeau du clown en 6 étapes

1. Construire un cercle de centre I, nommé ε.
2. Placez un diamètre [EC] du cercle ε.
3. Tracer M, tel que (IM) ⟘ (EC) et M ⋲ ε.
4. Tracer un arc de cercle de centre M.
5. Placer 2 points, O et P, sur cet arc.
6. Tracer le segment [OP].

On obtient alors le chapeau du clown : le pompon est le cercle ε et le chapeau est le triangle isocèle MOP de sommet principal M tel que MO=MP et de base [OP].

Le triangle équilatéral 

C'est un triangle qui a ses trois côtés de même longueur. 

Equi = égal
Latéral = côté 

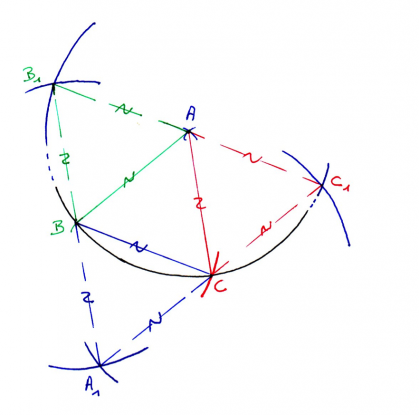
Une pyramide égyptienne 

A l'aide d'un compas, votre enfant peut s'entraîner à reproduire cette figure sur une feuille de papier : 

Chaque triangle obtenu est un triangle équilatéral : 

• ABC
• ABB1
• ACC1
• A1BC

Ils ont donc les côtés de même longueur.

Votre enfant, en pliant suivant les côtés [AB], [AC], [BC], obtient une pyramide à base équilatérale.

Le triangle rectangle

C'est un triangle qui comporte un angle droit. 

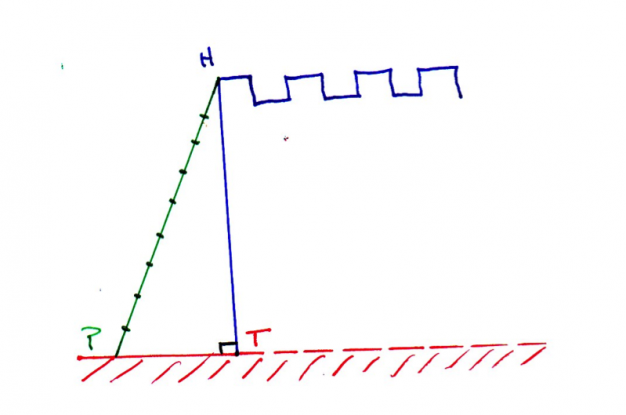
Une échelle pour attaquer le château fort. 

Pour construire une échelle afin d’attaquer le château fort, il faudra prendre la distance HP, en effet le triangle HPT est rectangle en T (symbolisé par l’angle droit ⦜).

Le mur du château fort et le terrain étant perpendiculaires : (HT)⟘(PT).

Donc pour grimper en haut du château (point H), il faudra parcourir la distance PH et donc fabriquer une échelle dont la « hauteur » mesure au moins cette longueur.

Et pour s'amuser à la maison ?