Mathématiques
Les translations en 4ème
Tout comme la symétrie axiale ou centrale, la translation, nouveauté du programme 2016, permet de transformer des figures.
Ici, la transformation est simple, puisqu’il s’agit de déplacer une figure et de la reconstruire à l’identique. Sa mise en œuvre est différente de la symétrie et nécessite de connaître les parallélogrammes.
Un exemple de translation
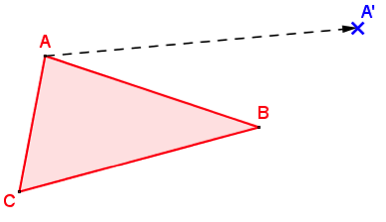
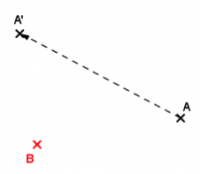
Voici un triangle ABC et un point A’.
A’ se lit « A prime ».
Comme on n’a pas le droit de placer deux points ayant le même nom, mais qu’on en a quand même besoin pour que l’énoncé reste clair, on utilise la notation A’ pour placer un « deuxième point A ».
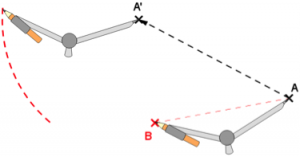
Nous allons étudier la translation qui transforme A en A’.
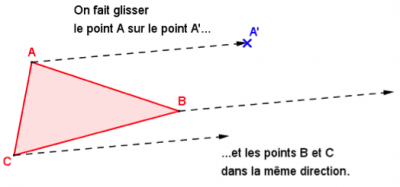
C’est-à-dire que nous allons « faire glisser » ou « déplacer » le triangle ABC de telle sorte que le point A et le point A’ soient superposés :
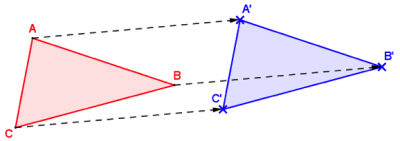
A l’arrivée, nous pouvons tracer un triangle A’B’C’, qui est l’image de ABC par la translation qui transforme A en A’.
Nous verrons un peu plus bas comment réaliser cette translation avec la règle et le compas.
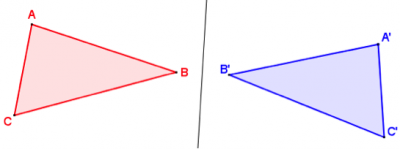
Contrairement à la symétrie, la figure n’est pas « retournée ».
Voici ce qu’aurait donné une symétrie axiale :
La translation a tout de même quelques points communs avec la symétrie :
- elle conserve les longueurs (si on translate un segment de 5 cm, son image mesurera aussi 5 cm)
- elle conserve les angles (si on translate un angle de 47°, son image mesurera aussi 47°)
Elle conserve également les alignements, et, comme la symétrie centrale, elle conserve le parallélisme.
Voyons maintenant comment réaliser une translation avec les instruments de géométrie.
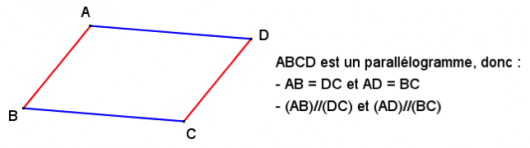
Les parallélogrammes
Votre enfant se rappelle sans doute des parallélogrammes : ce sont des quadrilatères dont les côtés opposés sont égaux et parallèles.
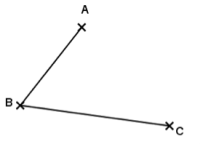
En 5ème, il a vu une méthode pour terminer le tracé d’un parallélogramme une fois que 3 points ont été placés :
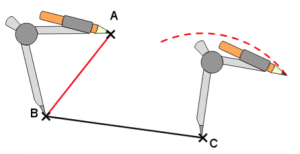
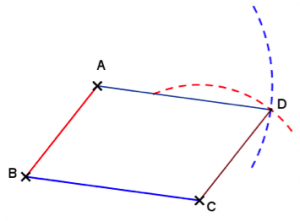
Au compas, on prend la longueur BA et on trace un arc de cercle de centre C…
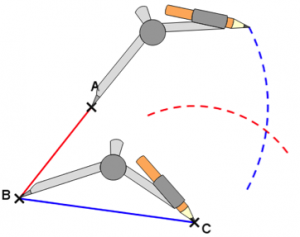
…ensuite, on prend la longueur BC et on trace un arc de cercle de centre A…
…puis on relie le point obtenu à A et C, et on peut l’appeler D pour obtenir le parallélogramme ABCD.
Translation à la règle et au compas
Tout cela est bien beau, mais quel rapport avec la translation ?
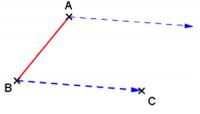
Revenons sur la figure précédente : imaginez qu’au lieu de tracer un parallélogramme, on ait voulu construire l’image du point A par la translation qui transforme B en C…
Les deux déplacements sont de même longueur et dans la même direction, donc parallèles.
Donc pour tracer l’image d’un point par une translation, il suffit de savoir tracer un parallélogramme !
Voyons cela sur un autre exemple : plaçons deux points A et A’, un point B, et essayons de tracer l’image de B par la translation qui transforme A en A’ :
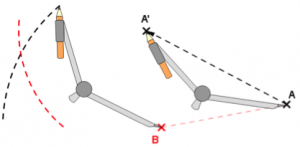
Au compas, on prend la distance AB, et on trace un arc de cercle de centre A’ :
Ensuite, on prend la distance AA’, et on trace un arc de cercle de centre B :
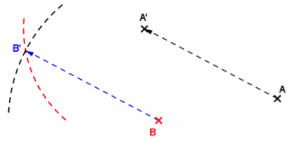
On obtient le point B’, qui est bien l’image de B par la translation qui transforme A en A’.
Une fois que votre enfant sait tracer l’image d’un point par une translation, il peut s’entraîner à tracer l’image de plusieurs points pour obtenir des triangles, des quadrilatères…
On peut aussi translater un cercle (il suffit de translater son centre) ou une droite (il suffit de placer deux points sur cette droite et de les translater).
Puisque translater revient à tracer un parallélogramme, il existe d’autres méthodes pour réaliser des translations, notamment en traçant des droites parallèles.
Tout comme les symétries, les translations sont plus faciles à réaliser sur papier quadrillé : pas besoin de règle ou de compas, il suffit juste de compter les carreaux !