Mathématiques
Les rotations en 4ème
Tout comme la symétrie, la rotation, nouveauté du programme 2016, permet de transformer des figures en les faisant tourner autour d’un point. C’est le moment de ressortir le compas et surtout le rapporteur, tout en revoyant la symétrie centrale.
Un exemple de rotation
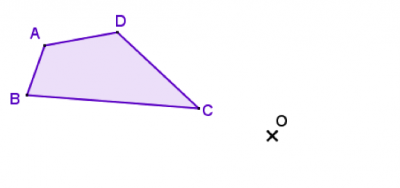
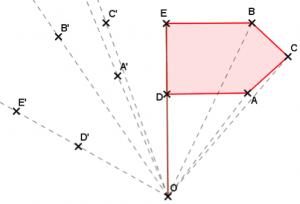
Voici un quadrilatère ABCD et un point O.
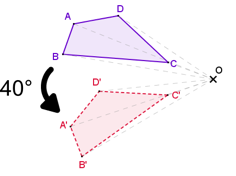
Intéressons-nous à l’image de ABCD par la rotation de centre O, d’angle 50° et de sens direct.
Cette transformation consiste à faire tourner le quadrilatère ABCD autour du point O, de 50°.
Vous vous demandez peut-être ce qu’est le sens direct : en mathématiques, « sens direct » signifie « sens inverse des aiguilles d’une montre ».
Nous pouvons nommer l’image A’B’C’D’.
A’ se lit « A prime ».
Comme on n’a pas le droit de placer deux points ayant le même nom, mais qu’on en a quand même besoin pour que l’énoncé reste clair, on utilise la notation A’ pour placer un « deuxième point A ».
On remarque que tout comme la symétrie centrale vue en 5ème, la rotation :
- conserve les longueurs (si on fait tourner un segment de 5 cm autour d’un point, son image mesurera aussi 5 cm)
- conserve les angles (si on fait tourner un angle de 47°, son image mesurera aussi 47°)
Elle conserve également les alignements et le parallélisme (deux droites parallèles le restent après une rotation).
D’ailleurs, la symétrie centrale est équivalente à une rotation d’angle 180° (angle plat).
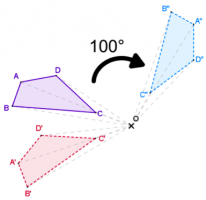
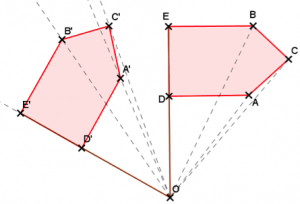
Étudions maintenant l’image de ABCD par la rotation de centre O, d’angle 100° et de sens indirect.
Cette fois, nous allons faire tourner ABCD autour de O, dans le sens des aiguilles d’une montre (indirect).
Nous pouvons nommer l’image A’’B’’C’’D’’. A’’ se lit « A seconde ».
Voyons maintenant comment appliquer de telles rotations avec le rapporteur.
Rotation au rapporteur
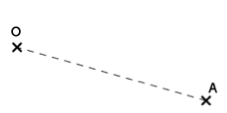
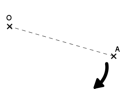
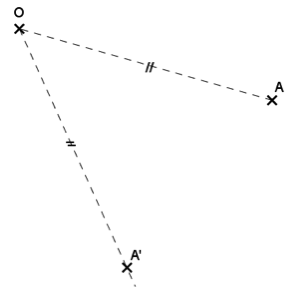
Commençons par tracer l’image d’un point A par une rotation de 50° et de sens indirect autour d’un point O.
Tout comme lors d’une symétrie centrale, on commence par relier le point A au point O (inutile cependant de prolonger le segment).
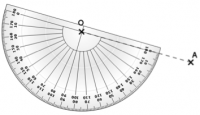
Vient ensuite le moment de placer le rapporteur, et là il faut faire très attention !
- on place le rapporteur sur O, car c’est le centre de la rotation
- on remarque que la rotation est de sens indirect, c’est-à-dire le sens des aiguilles d’une montre.
Imaginons que [OA] serait l’aiguille d’une horloge dont O serait le centre, comment tournerait A ?
On place donc le rapporteur en alignant la graduation 0° avec [OA] de telle sorte que les autres graduations soient orientées dans le sens indirect.
En plus clair : ici, on place le rapporteur en-dessous de [OA].
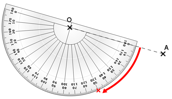
Comme lorsqu’on veut tracer un angle, on place un point au niveau de la graduation 50°.
Attention : il y a deux graduations 50° ! Il faut suivre celle qui correspond au 0° qui a été aligné avec le segment [OA].
On trace ensuite une demi-droite d’origine O dans la direction de ce point.
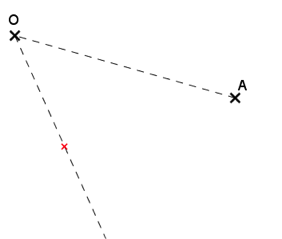
Et pour terminer, avec le compas (c’est mieux que la règle graduée), on reporte la distance OA sur cette demi-droite, et on place le point A’.
L’angle ainsi formé mesure 50°.
Un drapeau à agiter
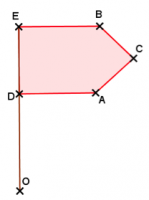
Considérons ce « drapeau ».
Traçons l’image du drapeau par la rotation de centre O, d’angle 60° et de sens direct.
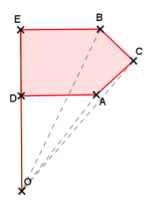
On commence par tracer [OA], [OB] et [OC] (D et E sont déjà reliés à O).
Avec le rapporteur, on forme plusieurs angles de 60° avec les segments [OA], [OB]…
Attention à bien les faire en plaçant le rapporteur sur O, en alignant la graduation 0° avec les segments et en plaçant le rapporteur du bon côté (ici, à gauche des segments).
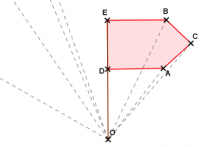
On reporte ensuite les distances OA, OB… sur les demi-droites...
Et on relie les points !