La réciproque de Pythagore est un outil permettant, si on connaît les trois côtés d’un triangle, de démontrer qu’il est rectangle.

Attention à ne pas confondre théorème et réciproque :

• le théorème s’applique lorsqu’on sait que le triangle est rectangle et qu’on veut calculer la longueur d’un côté
• la réciproque s’applique lorsqu’on connait les longueurs des côtés et qu’on veut démontrer que le triangle est rectangle.

Pour cette raison, on ne peut donc pas appliquer le théorème de Pythagore et sa réciproque, en même temps, dans le même triangle (ce qui peut arriver en revanche avec la réciproque du théorème de Thalès).

Un premier exercice de construction 

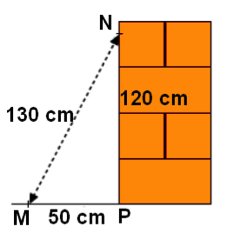
« Un maçon cherche à construire un mur perpendiculaire au sol. Une fois le mur construit, il effectue les mesures suivantes :

Le mur est-il bien perpendiculaire au sol ? Justifier. »

On connaît toutes les longueurs d’un triangle ? On cherche à savoir si un angle est droit ? On applique la réciproque de Pythagore ! 

Notre mission est donc de montrer que le carré d’un côté (le plus long) est égal à la somme des carrés des deux autres.

Le plus long côté est MN. Nous allons donc calculer MN² d’une part, et PM² + PN² d’autre part.

MN² = 130² = 16 900
PM² + PN² = 50² + 120² = 2 500 + 14 400 = 16 900
On constate que MN² = PM² + PN². D’après la réciproque du théorème de Pythagore, le triangle PMN est rectangle en P.
Ainsi, le mur est bien perpendiculaire au sol !

Notez que tant qu’on n’a pas montré que le triangle est rectangle, on ne parle pas d’ « hypoténuse », mais de « côté le plus long ». 

La contraposée