Aires et périmètres des rectangles et carrés

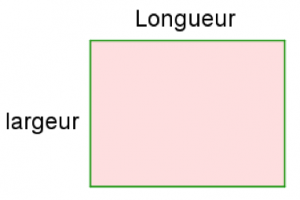
Votre enfant sait sans doute calculer l’aire d’un rectangle depuis longtemps, mais il arrive encore, en 4^ème, qu’il y ait des confusions entre aire et périmètre. Voici donc un rappel sur les rectangles.

• Le périmètre est égal à 2 × Longueur + 2 × largeur, ou bien 2 × (Longueur + largeur).

En effet, un rectangle comporte « deux longueurs et deux largeurs ».
Les deux formules sont équivalentes, la distributivité permet de passer de l’une à l’autre.
On peut aussi réécrire ces formules sans signe × et en utilisant les lettres L et l : 2L + 2l ou bien 2(L + l).

• L’aire est égale à Longueur × largeur, soit L × l.

Cela se comprend par exemple en traçant un rectangle de longueur 7 cm et de largeur 4 cm :

Ici, 1 carreau représente 1 cm², l’aire en cm² est égale au nombre de carreaux. 
Or, pour trouver le nombre de carreaux, il suffit de multiplier le nombre de carreaux en longueur par le nombre de carreaux en largeur, c’est-à-dire 7 × 4 = 28 cm².

Calculer l’aire d’un rectangle revient donc àmultiplier sa longueur par sa largeur.

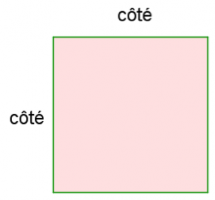
Le carré est un cas particulier du rectangle.

Dans un carré, la longueur et la largeur sont identiques, on les appelle donc le côté du carré.

La formule du périmètre devient 4 × côté (un carré ayant 4 côtés identiques), autrement dit 4c.
La formule de l’aire devient côté × côté, qu’on notera c × c ou mieux, c².

Par exemple, l’aire d’un carré de côté 5 cm est égale à 5² = 5 × 5 = 25 cm².

La fiche sur la racine carrée contient d’autres explications sur la notation « ² ».

Aires et périmètres des triangles

Le périmètre d’un triangle s’obtient en additionnant les longueurs des côtés. Il n’y a pas, en général, d’autre méthode plus efficace.

En revanche, le calcul de l’aire est plus technique !

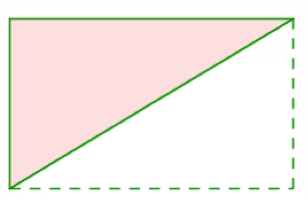
Commençons par le triangle rectangle, qui s’obtient grâce à l’aire d’un rectangle.
En effet, un triangle rectangle est la « moitié » d’un rectangle !

Pour trouver l’aire du triangle rectangle, il suffit donc de calculer l’aire du rectangle entier, puis de diviser le résultat par 2.

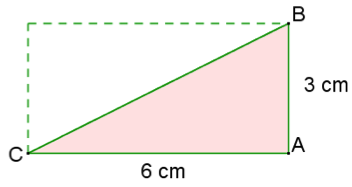
Ainsi, pour ce triangle ABC rectangle en A tel que AB = 6 cm et AC = 3 cm :

A = (6 × 3) ÷ 2 = 18 ÷ 2 = 9 cm².

Notez que la mesure du côté opposé à l’angle droit (l’hypoténuse) ne sert ici à rien.

Dans le cas d’un triangle non rectangle, on peut (presque) utiliser cette méthode !

Aires et périmètres des rectangles et carrés

Votre enfant sait sans doute calculer l’aire d’un rectangle depuis longtemps, mais il arrive encore, en 4^ème, qu’il y ait des confusions entre aire et périmètre. Voici donc un rappel sur les rectangles.

• Le périmètre est égal à 2 × Longueur + 2 × largeur, ou bien 2 × (Longueur + largeur).

En effet, un rectangle comporte « deux longueurs et deux largeurs ».
Les deux formules sont équivalentes, la distributivité permet de passer de l’une à l’autre.
On peut aussi réécrire ces formules sans signe × et en utilisant les lettres L et l : 2L + 2l ou bien 2(L + l).

• L’aire est égale à Longueur × largeur, soit L × l.

Cela se comprend par exemple en traçant un rectangle de longueur 7 cm et de largeur 4 cm :

Ici, 1 carreau représente 1 cm², l’aire en cm² est égale au nombre de carreaux. 
Or, pour trouver le nombre de carreaux, il suffit de multiplier le nombre de carreaux en longueur par le nombre de carreaux en largeur, c’est-à-dire 7 × 4 = 28 cm².

Calculer l’aire d’un rectangle revient donc àmultiplier sa longueur par sa largeur.

Le carré est un cas particulier du rectangle.

Dans un carré, la longueur et la largeur sont identiques, on les appelle donc le côté du carré.

La formule du périmètre devient 4 × côté (un carré ayant 4 côtés identiques), autrement dit 4c.
La formule de l’aire devient côté × côté, qu’on notera c × c ou mieux, c².

Par exemple, l’aire d’un carré de côté 5 cm est égale à 5² = 5 × 5 = 25 cm².

La fiche sur la racine carrée contient d’autres explications sur la notation « ² ».

Aires et périmètres des triangles