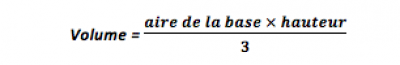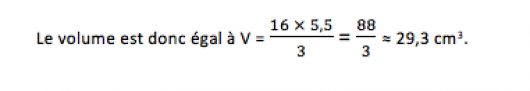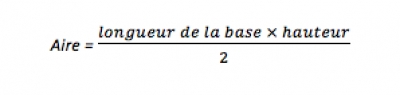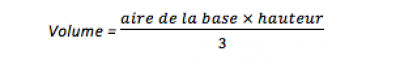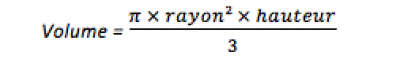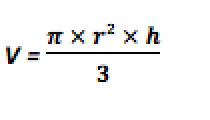Les calculs de volumes sont souvent abordés au Brevet, c’est pourquoi il est important de connaître et d’utiliser toutes les formules de calcul de volume en fin de 3^ème. 

Pavé droit

Un pavé droit est un solide délimité par six faces rectangulaires. 

Il possède 3 dimensions : hauteur, largeur et Longueur.
Le volume d’un pavé droit est égal au produit de ces trois dimensions :

Volume = hauteur × largeur × Longueur

Si on appelle h la hauteur, l la largeur et L la Longueur, on écrira V = h × l × L. 

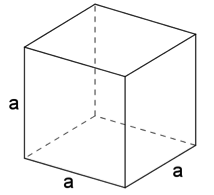
Cube

Un cube est un pavé droit dont toutes les faces sont carrées. 
La hauteur, la largeur et la longueur étant identiques, un cube n’a qu’une dimension, appelée arête.

Le volume d’un cube est donc égal à : 

Volume = arête × arête × arête

On préfère l’écrire avec une puissance : si a est l’arête d’un cube, et V son volume :

V = a × a × a = a³

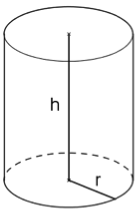
Cylindre

Un cylindre de révolution est un solide composé de :

• deux disques parallèles et superposables, appelés les bases,
• une face courbe, qu’on peut assimiler à un « rectangle enroulé » : le patron d’un cylindre est d’ailleurs constitué de de deux disques et d’un rectangle qu’on enroule autour de ces deux disques.

On l’appelle cylindre de révolution car on peut l’obtenir en « faisant tourner » un rectangle autour de l’un de ses côtés.

Un cylindre a deux dimensions : sa hauteur, et le rayon de ses disques de base.

Son volume est égal au produit de l’aire de la base par la hauteur

Volume = aire de la base × hauteur

Toutefois, la base est un disque. L’aire d’un disque est égale à : π × rayon² 
Ainsi, le volume d’un cylindre est égal à :

Volume = π × rayon² × hauteur

Si on appelle r le rayon et h la hauteur, V = π × r² × h

Ne pas oublier que le carré d’un nombre est égal au produit de ce nombre par lui-même. Par exemple, 5² = 5 × 5 = 25, et 1,5² = 1,5 × 1,5 = 2,25.
Le carré ne doit pas être confondu avec le double : 5² n’est pas égal à 10.

Pyramide

Une pyramide est constituée :

• d’un polygone appelé la base
• de plusieurs faces triangulaires qui relient les côtés de la base au sommet

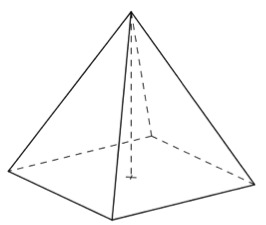
Cette pyramide est régulière (comme les pyramides d’Égypte) : sa base est un carré, qui est un polygone régulier (tous ses côtés et tous ses angles sont égaux) et les triangles qui relient la base au sommet sont isocèles.

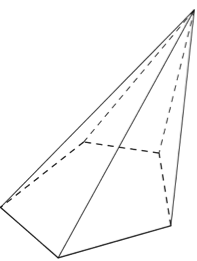
Mais il est tout à fait possible qu’une pyramide ne soit pas régulière, notamment le sommet n’est pas toujours « au-dessus » de la base, comme ci-dessous :

Le volume d’une pyramide est le produit de l’aire de la base par la hauteur, divisé par 3.

Il faut donc calculer l’aire de la base de la pyramide avant d’en déduire le volume.

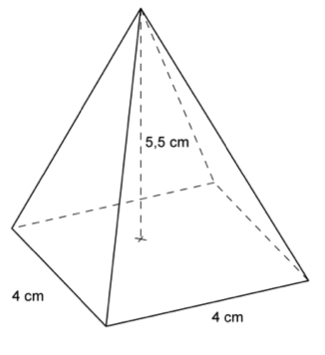
Calculons le volume de la pyramide ci-dessous 

La base est un carré, dont l’aire est égale à 4 × 4 = 16 cm².
La hauteur est de 5,5 cm.

Les pyramides (et les cônes) sont aussi l’objet d’un travail sur l’agrandissement et la réduction de figures, dont un exemple est donné dans la fiche sur l’homothétie.

Attention à ne pas confondre la formule du volume d’une pyramide avec la formule de l’aire d’un triangle, qui est :

Cône

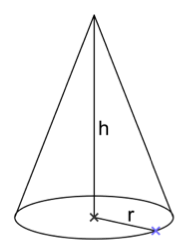
Un cône de révolution est constitué :

• d’un disque appelé la base
• d’un secteur angulaire « enroulé » autour de ce disque

On peut obtenir un cône en « faisant tourner » un triangle rectangle autour d’un des côtés de l’angle droit, d’où l’appellation « cône de révolution ».

Un cône a deux dimensions : sa hauteur, et le rayon du disque de base.

La formule du volume d’un cône est la même que celle de la pyramide :

Toutefois, la base est un disque. L’aire d’un disque est égale à : π × rayon² 
Ainsi, le volume d’un cône est égal à :

Si on appelle r le rayon et h la hauteur

Sphère et boule