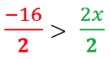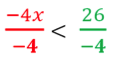Maths
Comprendre les inéquations
Équation ou inéquation ?
Le retour des équations
L’année de 4ème a été l’occasion de résoudre des équations : ce sont des égalités comportant des nombres inconnus. On peut les voir comme des égalités à trous. Elles permettent de résoudre des problèmes plus complexes qu’en 6ème et 5ème.
Par exemple, 2x + 5 = 3x + 1 est une équation. Le nombre inconnu est représenté par la lettre x.
Sa solution, c’est-à-dire le nombre qu’on peut écrire à la place de x, est 4, car si on remplace x par 4
2x + 5 = 2 × 4 + 5 = 13 et
3x + 1 = 3 × 4 + 1 = 13
Comme les deux calculs sont égaux, 4 est bien la solution de cette équation. La méthode permettant de trouver la solution des équations est vue en 4ème.
Et les inéquations ?
C’est presque identique !
Une inéquation est une inégalité comportant des nombres inconnus.
2x + 5 > 3x + 1 est une inéquation.
A la place du signe = (égal), une inéquation comporte un des symboles suivants :
- > (supérieur à)
- ≥ (supérieur ou égal à)
- < (inférieur à)
- ≤ (inférieur ou égal à)
Une infinité de solutions
Là où les équations vues au collège n’ont souvent qu’une seule solution, les inéquations peuvent avoir une infinité de solutions !
Ainsi, pour l’inéquation 2x + 5 > 3x + 1 , n’importe quel nombre inférieur à 4 convient.
- Si x = 3
2x + 5 = 2 × 3 + 5 = 11 et 3x + 1 = 3 × 3 + 1 = 10.
11 > 10 , donc 3 est une solution.
- Si x = 1
2x + 5 = 2 × 1 + 5 = 7 ; et 3x + 1 = 3 × 1 + 1 = 4.
7 > 4 , donc 1 est une solution.
- Par contre, prenons x = 6
2x + 5 = 2 × 6 + 5 = 17 ; et 3x + 1 = 3 × 6 + 1 = 19.
17 < 19, donc 6 n’est pas une solution.
Pour résoudre une inéquation, on utilise la même méthode que pour les équations (à une exception près, voir plus bas !)
Des problèmes à résoudre
Pourquoi s’embêter avec les inéquations alors que les équations existent déjà ? C’est parce qu’elles ne permettent pas de résoudre les mêmes problèmes !
Problème résolu avec une équation
« Magali achète 5 cahiers et un livre. Elle paie au total 19,60 €.
Sachant que le prix du livre est 12 €, quel est le prix d'un classeur ? »
Ici, on cherche bien un seul nombre inconnu : le prix d’un classeur, que l’on appelle x.
Le problème se met en équation de la façon suivante : 5x + 12 = 19,60
Problème résolu avec une inéquation
Une société compare les tarifs de deux transporteurs :
- l'entreprise « Vitlivré» propose une somme de 2,50 € par km parcouru,
- l'entreprise « Rapido » propose un forfait de 160 € puis une somme de 1,70 € par km parcouru.
À partir de quel kilométrage l'entreprise « Rapido » est-elle la plus intéressante ?
Ici, on veut comparer deux prix, et déterminer pour quel kilométrage le prix de l’entreprise « Rapido » est le plus petit.
Si on appelle x le nombre de km parcourus, cela correspond à l’inéquation 160 + 1,70 x < 2,50 x
Comment résoudre une inéquation ?
Tout comme avec les équations, on peut effectuer la même opération aux deux membres d’une inéquation. Ceci permet de la « transformer » jusqu’à obtenir la solution.
| Ainsi en partant de l’inéquation : | x + 2 > 3x + 18 |
|
| On soustrait x aux deux membres | x + 2 – x > 3x + 18 – x |
|
| l’inéquation devient | 2 > 2x+ 18 |
|
On soustrait 18 aux deux membres, l’inéquation devient : 2 – 18 > 2x + 18 – 18
puis : – 16 > 2x
On divise les deux membres par 2, l'inéquation devient :
puis : – 8 > x
Les solutions sont tous les nombres inférieurs à -8.
Attention : il y a tout de même une petite difficulté supplémentaire
Si on multiplie ou divise les deux membres par un nombre négatif, ou si on change le signe des deux membres, le sens de l’inéquation change aussi !
Ainsi, si on doit résoudre : – 4x > 26
on divise les deux membres par -4, l’inéquation devient :
puis : x < – 6,5
Et si on résout : 7 ≤ – x
on change le signe des deux membres et l’inéquation devient : – 7 ≥ x
Droites graduées
Une fois qu’on a trouvé les solutions d’une inéquation, on peut les représenter sur une droite graduée.