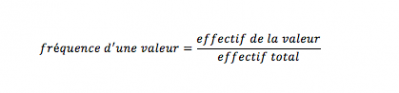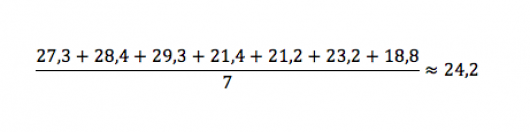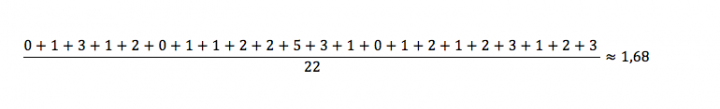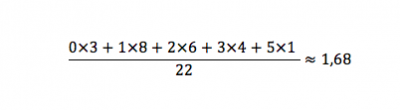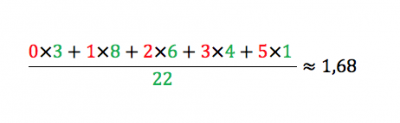Mathématiques
Les statistiques en 4ème
Les statistiques sont étudiées pendant les trois années du cycle 4.
En 4ème, c’est l’occasion d’aborder la fréquence. On étudie aussi les moyennes simples et pondérées, ce qui permettra enfin à vos enfants de comprendre comment sont calculées les moyennes de leur bulletin !
Il est possible que des professeurs décident de laisser la moyenne pondérée pour la 3ème, ou au contraire commencent la médiane en 4ème. Si c'est le cas, cliquez sur la fiche des statistiques en 3ème.
Vocabulaire
En statistiques, on étudie des caractères propres à chaque individu d’une population.
Par exemple, on peut étudier l’âge (c’est le caractère) des téléspectateurs d’une émission (c’est la population).
Le caractère étudié est souvent quantitatif (on relève un nombre comme l’âge, la taille etc…) mais il est parfois qualitatif (la couleur des yeux, le sport pratiqué…)
Un ensemble de données collectées s’appelle une série statistique. Par exemple, si on relève le nombre d’enfants de différentes familles, on peut obtenir la série statistique suivante :
0 ; 1 ; 3 ; 1 ; 2 ; 0 ; 1 ; 1 ; 2 ; 2 ; 5 ; 3 ; 1 ; 0 ; 1 ; 2 ; 1 ; 2 ; 3 ; 1 ; 2 ; 3
On a relevé 22 valeurs : 22 est appelé l’effectif total.
Cette série peut se représenter dans un tableau d’effectifs…
| Nombre d'enfants | 0 | 1 | 2 | 3 | 4 | 5 |
| Effectifs | 3 | 8 | 6 | 4 | 0 | 1 |
…qui signifie par exemple que 3 familles interrogées ont 0 enfant, 8 familles interrogées en ont 1, et ainsi de suite.
Fréquence
La fréquence d’une valeur est un nombre (compris entre 0 et 1) ou un pourcentage (de 0% à 100%) qui indique à quelle fréquence cette valeur est présente dans la série.
Elle se calcule en divisant l’effectif d’une valeur par l’effectif total :
Ainsi, dans la série du nombre d’enfants, sur 22 familles interrogées, quatre familles avaient 3 enfants. La fréquence de la valeur 3 est égale à 4 ...... 22 ≈0,18.
De même, sur 22 familles interrogées, six familles avaient 2 enfants. La fréquence de la valeur 2 est égale à 6 ...... 22 ≈0,27.
On peut dresser un tableau de fréquences :
| Nombre d'enfants | 0 | 1 | 2 | 3 | 4 | 5 |
| Effectifs | 3 | 8 | 6 | 4 | 0 | 1 |
| Fréquences | 0,14 | 0,36 | 0,27 | 0,18 | 0 | 0,05 |
Pour obtenir les fréquences en pourcentage, il suffit de les multiplier par 100, ce qui revient à décaler leur virgule de deux rangs.
| Nombre d'enfants | 0 | 1 | 2 | 3 | 4 | 5 |
| Effectifs | 3 | 8 | 6 | 4 | 0 | 1 |
| Fréquences (%) | 14 | 36 | 27 | 18 | 0 | 5 |
Moyenne simple
La moyenne est un indicateur d’une série statistique, qui correspond à une répartition identique des valeurs.
Plus concrètement, voici les températures en °C relevées à 15h chaque jour d’une semaine du mois d’août, à Paris :
27,3 ; 28,4 ; 29,3 ; 21,4 ; 21,2 ; 23,2 ; 18,8
Pour calculer la moyenne, il suffit d’additionner toutes ces températures, puis de diviser cette somme par l’effectif total (qui est égal à 7, car on a relevé 7 températures) :
La moyenne est de 24,2°C (arrondie au dixième). Cela signifie que si la température avait été équitablement répartie entre ces 7 jours, il aurait fait 24,2°C toute la semaine.
Avec la série des enfants dans différentes familles :
0 ; 1 ; 3 ; 1 ; 2 ; 0 ; 1 ; 1 ; 2 ; 2 ; 5 ; 3 ; 1 ; 0 ; 1 ; 2 ; 1 ; 2 ; 3 ; 1 ; 2 ; 3
L’effectif total étant 22, le calcul est plus long à écrire:
En remarquant que le 1 revient 8 fois, le 2 revient 6 fois, etc… on peut écrire un calcul plus joli :
Ce type de calcul s’appelle une moyenne pondérée.
Moyenne pondérée
On fait une moyenne pondérée quand chaque valeur est affectée d’un « poids » (d’où l’adjectif « pondérée »).
Avec des effectifs
Par exemple, en se basant sur le tableau d’effectifs en début de fiche :
| Nombre d'enfants | 1 | 2 | 3 | 4 | 5 | |
| Effectifs | 3 | 8 | 6 | 4 | 1 |
Ici, le « poids » correspond aux effectifs.
On calcule la moyenne en multipliant chaque valeur par l’effectif correspondant, puis en divisant par l’effectif total (la somme des effectifs) :
Avec des coefficients
Le principe est le même avec des coefficients (c’est une question qui revient très souvent en classe !).