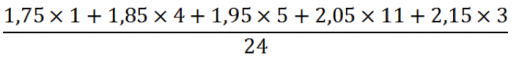Mathématiques
Regroupement par classes : les statistiques en 3ème
Les regroupements par classes permettent de simplifier le calcul de la moyenne ou de la médiane lorsque les données sont toutes différentes. Il est important de les maîtriser pour comprendre et analyser les statistiques qui nous sont proposées dans les médias ou ailleurs.
En statistiques, il arrive que les valeurs soient toutes différentes les unes des autres.
En guise d'exemple, pour toute cette fiche, prenons la taille des 24 joueurs présélectionnés pour l’équipe de France de basketball lors de la Coupe du Monde 2014 :
2,15 ; 1,78 ; 2,03 ; 1,84 ; 2,02 ; 1,93 ; 1,95 ; 2,03 ; 1,87 ; 1,99 ; 2,00 ; 2,13 ; 1,88 ; 1,88 ; 1,99 ; 2,09 ; 2,02 ; 2,00 ; 2,14 ; 2,01 ; 2,06 ; 1,99 ; 2,07 ; 2,05
Un tableau d’effectifs classique serait très long et comporterait beaucoup de cases avec un effectif de 1 ou 2, ce qui serait encore moins clair que la liste.
On peut toutefois regrouper les joueurs en les répartissant en 5 « classes » suivant leur taille :
- entre 1,70 m et 1,80 m (on exclut ici ceux dont la taille est 1,80 m),
- entre 1,80 m et 1,90 m (idem, on exclut ici ceux dont la taille est 1,90 m),
- etc…
Ces 5 classes peuvent se noter avec des crochets :[1,70 ; 1,80[ ; [1,80 ; 1,90[ ; [1,90 ; 2,00[ ; [2,00 ; 2,10[ ; [2,10 ; 2,20[
Attention au placement des crochets : la classe [1,80 ; 1,90[ signifie qu’on prend les joueurs entre 1,80 m et 1,90, en incluant ceux qui mesurent exactement 1,80 m (car le crochet est orienté vers le nombre) mais en excluant ceux qui mesurent 1,90 m (car le crochet est orienté dans l’autre sens !)
Un joueur qui mesure 1,90 m se retrouvera plutôt dans la classe [1,90 ; 2,00[.
Moyenne
Pour calculer la moyenne lorsqu’on ne dispose que du regroupement par classes (et pas de la liste avec les « vraies » valeurs), il faut supposer que tous les membres d’une classe correspondent à la même valeur.
Par exemple, comme on ne peut pas savoir, dans la classe [1,80 ; 1,90[ , la taille réelle des 4 joueurs, on supposera qu’ils mesurent tous 1,85 m (la moyenne de 1,80 et 1,90). Ce nombre, 1,85, est appelé le centre de la classe.
Pour s’aider, on peut compléter le tableau avec les centres des classes :
Puis, calculer une moyenne pondérée :
La taille moyenne des joueurs est d’environ 2,00 m.
Médiane
Pour calculer la médiane, on fait comme d’habitude :
- on calcule l’effectif total : 1 + 4 + 5 + 11 + 3 nous donne 24 (il y a en tout 24 joueurs)
- on divise l’effectif total par deux : 24 ÷ 2 = 12. Comme l’effectif total est pair, la médiane est donc la moyenne de la 12ème et de la 13ème valeur.
- on rajoute une ligne avec les effectifs cumulés croissants :
La classe contenant la 12ème et la 13ème valeur est [2,00 ; 2,10[. On l’appelle la classe médiane.
Étendue
Pour calculer l'étendue, on prend la plus grande valeur des classes (2,20) et on lui soustrait la plus petite (1,70).
Une valeur approchée de l’étendue est donc 2,20 – 1,70 = 0,50 m.
Pour avoir la valeur exacte, il faudrait travailler avec la liste de nombres.